Using Z-Score in Trading — A Python Study.

Creating a Trading Strategy Based on the Z-Score Indicator.

Normalization is a technique that scales the time series and attempts to make it stationary. Normalization can take many forms, among them, the z-score method which is the protagonist of this article. We want to see what is z-score, how to code it, and how to use it in trading.

I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.

The Normalization Technique

We have to understand two things about technical indicators:

• They are price derived. this means that they take the price and decompose it to understand some characteristics. They are therefore not forward looking but backward looking. Our hope is for this backward relationship to continue in the future. For example, if we see a divergence on the RSI, we are hoping it causes exhaustion in prices like it usually does. This divergence does not peek at the future, it is simply a mathematical observation.

• They are unlikely to provide a winning strategy on their own. If they did, then why aren’t we all millionaires depending on overbought/oversold zones on the Stochastic indicator? Trading is much more complicated than that and requires a more thorough approach to find profitable trades.

With that being in mind, we should think of indicators as little helpers with our convictions. For example, when we find sufficient information to tell us to go long (buy) an asset, we can check the technical indicators to see whether they confirm this or not. We should also check the current market state to know whether the indicator is going to provide a good signal or not.

Normalization is simply a mathematical calculation that uses the scales data. This great technique allows us to trap the values between 0 and 1 (or 0 and 100 if we wish to multiply by 100). One famous example of normalization (or data featuring) revolves around subtracting the minimum value in a certain lookback period from the current value and dividing by the maximum value in the same lookback period minus the minimum value (the same in the nominator).

Let us first code the primal functions that are needed to facilitate data manipulation and modification.

# The function to add a certain number of columns
def adder(Data, times):
    
    for i in range(1, times + 1):
    
        z = np.zeros((len(Data), 1), dtype = float)
        Data = np.append(Data, z, axis = 1)                
    return Data

# The function to deleter a certain number of columns
def deleter(Data, index, times):
    
    for i in range(1, times + 1):
    
        Data = np.delete(Data, index, axis = 1)               
    
    return Data

# The function to delete a certain number of rows from the beginning
def jump(Data, jump):
    
    Data = Data[jump:, ]
    
    return Data
def normalizer(Data, lookback, what, where):
        
    for i in range(len(Data)):
        
        try:
            Data[i, where] = (Data[i, what] - min(Data[i - lookback + 1:i + 1, what])) / (max(Data[i - lookback + 1:i + 1, what]) - min(Data[i - lookback + 1:i + 1, what]))
        
        except ValueError:
            pass
    
    Data[:, where] = Data[:, where] * 100    
    Data = jump(Data, lookback)    
    return Data

EURUSD in the first panel with the 4-period Normalized Index in the second panel.

Intuitively, we can understand that when the 4-period Normalized Index is at 100, it means that the current close of the market price is the highest during the last 4 periods. Now, we will see another type of normalization called the Z-score.

The Z-Score Method

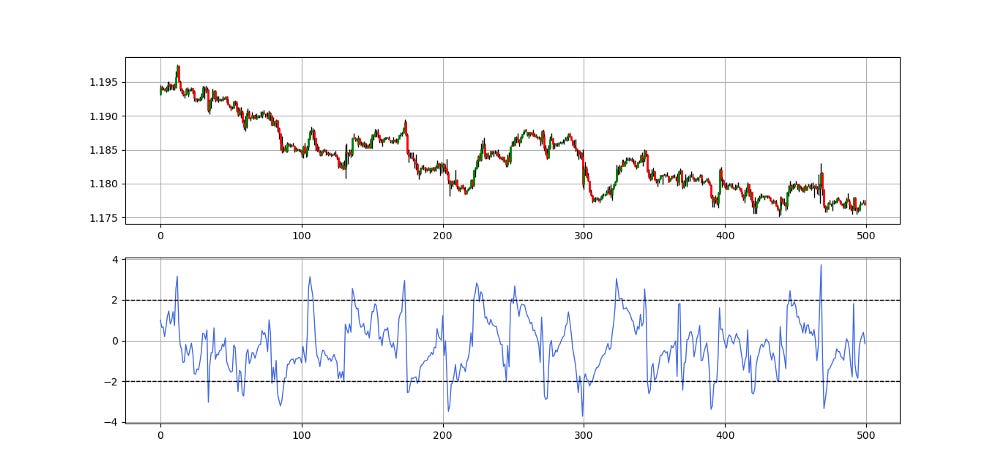
The Z-score measures the current analyzed value relative to its mean in terms of how many standard deviation away. The Z-score is easily interpreted this way:

• If the Z-score is 0, it indicates that the data point’s score is the same as the mean’s score.

• If the Z-score is 1.0 would indicate a value that is one standard deviation above the mean.

• If the Z-score is -1.0 would indicate a value that is one standard deviation below the mean.

To calculate the Z-score, we must use the below formula:

EURUSD hourly values in the first panel with the 21-period Z-score in the second panel.

def z_score_indicator(Data, ma_lookback, std_lookback, close, where):
    
    # Adding Columns
    Data = adder(Data, 1)
    
    # Calculating the moving average
    Data = ma(Data, ma_lookback, close, where)
    
    # Calculating the standard deviation
    Data = volatility(Data, std_lookback, close, where + 1)
    
    # Calculating the Z-Score
    for i in range(len(Data)):
        
      Data[i, where + 2] = (Data[i, close] - Data[i, where]) / Data[i, where + 1]
        
    # Cleaning
    Data = deleter(Data, where, 2)
    
    return Data

We can derive contrarian trading rules from the definition of the indicator such as the following:

• Go long (Buy) whenever the 21-period Z-score reaches -2.0.

• Go short (Sell) whenever the 21-period Z-score reaches 2.0

Signal chart on the EURUSD.

The function to create the signals can be written down as follows:

# Calculating the 21-period Z-score
my_data = z_score_indicator(my_data, 21, 21, 3, 4)

def signal(Data, what, buy, sell):
    
    Data = adder(Data, 10)
        
    for i in range(len(Data)):
            
        if Data[i, what] <= lower_barrier and Data[i - 1, buy] == 0 and Data[i - 2, buy] == 0 and Data[i - 3, buy] == 0 and Data[i - 4, buy] == 0:
            Data[i, buy] = 1
            
        elif Data[i, what] >= upper_barrier and Data[i - 1, sell] == 0 and Data[i - 2, sell] == 0 and Data[i - 3, sell] == 0 and Data[i - 4, sell] == 0:
            Data[i, sell] = -1    
            
    return Data

lower_barrier = -2
upper_barrier =  2

my_data= signal(my_data, 4, 6, 7)

Signal chart on the USDCHF.

Without a doubt, the Z-score indicator is not a perfect strategy as it tends to perform worse in trending markets, but it remains an interesting technique to know alongside the regular normalization technique we are used to.

Signal chart on the EURCHF.

If you are interested by market sentiment and how to model the positioning of institutional traders, feel free to have a look at the below article:

Conclusion

Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.

I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing Back-testing results should lead the reader to explore more herself the strategy and work on it more. That way you can share with me your better strategy and we will get rich together.

To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.