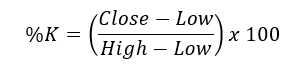Using Exponential Smoothing in Creating a Technical Indicator
Creating an Exponential Smoothing Indicator to Trade the Market in Python
Smoothing or averaging is a form of noise reduction that traders use to get a clearer picture on the trend or on extreme moves. The stochastic oscillator is known to have a signal line called the %D where a simple moving average is applied to the stochastic formula so that it makes it smoother. In this article, we will create a stochastic oscillator entirely made out of exponential moving averages.
It is finally out! My newest book with O’Reilly Media on candlestick pattern recognition is now available on Amazon! The book features a huge number of classic and modern candlestick patterns as it dwelves into the realm of technical analysis with different trading strategies. The book comes with its own GitHub and is dynamic in nature as it is continuously updated and questions are answered on the O’Reilly platform.
Mastering Financial Pattern Recognition
Amazon.com: Mastering Financial Pattern Recognition eBook : Kaabar, Sofien: Kindle Storewww.amazon.com
The Concept of Moving Averages
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
As the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
We can see that the moving average is providing decent dynamic support and resistance levels from where we can place our orders in case the market goes down there. The code for the moving average can be written down as the following:
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data fileThe below states that the moving average function will be called on the array named my_data for a lookback period of 200, on the column indexed at 3 (closing prices in an OHLC array). The moving average values will then be put in the column indexed at 4 which is the one we have added using the adder function.
my_data = ma(my_data, 200, 3, 4)An exponential moving average is a special type that gives more weight to the recent values. To spare you the boring details, here is the code.
def ema(data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
data = ma(data, lookback, what, where)data[lookback + 1, where] = (data[lookback + 1, what] * alpha) + (data[lookback, where] * beta)for i in range(lookback + 2, len(data)):
try:
data[i, where] = (data[i, what] * alpha) + (data[i - 1, where] * beta)
except IndexError:
pass
return dataThe Stochastic Smoothing Oscillator
First, let us start by the usual stochastic oscillator before proceeding with the stochastic smoothing oscillator. The stochastic oscillator seeks to find oversold and overbought zones by incorporating the highs and lows using a normalization formula as shown below:
An overbought level is an area where the market is perceived to be extremely bullish and is bound to consolidate. An oversold level is an area where market is perceived to be extremely bearish and is bound to bounce. Hence, the stochastic oscillator is a contrarian indicator that seeks to signal reactions of extreme movements. We will create the below function that calculates the stochastic on an OHLC data:
def stochastic_oscillator(data,
lookback,
high,
low,
close,
where,
slowing = False,
smoothing = False,
slowing_period = 1,
smoothing_period = 1):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = (data[i, close] - min(data[i - lookback + 1:i + 1, low])) / (max(data[i - lookback + 1:i + 1, high]) - min(data[i - lookback + 1:i + 1, low]))
except ValueError:
pass
data[:, where] = data[:, where] * 100
if slowing == True and smoothing == False:
data = ma(data, slowing_period, where, where + 1)
if smoothing == True and slowing == False:
data = ma(data, smoothing_period, where, where + 1)
if smoothing == True and slowing == True:
data = ma(data, slowing_period, where, where + 1)
data = ma(data, smoothing_period, where, where + 2)
data = jump(data, lookback)return data
The above plot shows the EURUSD values plotted with a 14-period Stochastic Oscillator. Notice that the indicator will always be bounded between 0 and 100 due to the nature of its normalization function that traps values between the minimum and the maximum.
Now, to get the stochastic smoothing oscillator, we can follow the below steps:
Calculate a n-period exponential moving average on the highs.
Calculate a n-period exponential moving average on the lows.
Calculate a n-period exponential moving average on the close.
Apply the stochastic formula on the above results.

my_data = ema(my_data, 2, 3, 1, 4)
my_data = ema(my_data, 2, 3, 2, 5)
my_data = ema(my_data, 2, 3, 3, 6)my_data = stochastic_oscillator(my_data, lookback, 4, 5, 6, 7)If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.