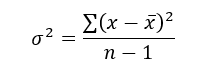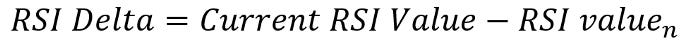Trading A-Z #4: The Relative Strength Index.
Article #4 on the Relative Strength Index and How to Use it Optimally.
The Relative Strength Index is one of the most common indicators in Technical Analysis. It allows us to have a quick glance as to whether the market is overbought or oversold. As controversial as this indicator is, its utility is well known and many strategies can be formed around. A good number of such strategies are stable and profitable ones. In this article, we will build the indicator from scratch and discuss some of its simple strategies as well as other variations on the RSI.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
Building the Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. Also, the fact that it is famous, contributes to its potential. This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. It is based on the idea of normalizing the smoothed momentum. The steps are therefore:
We must calculate the difference between the current closing price and the previous closing price.
Create two columns where the first column has the positive differences and the second column has the absolute values of the negative differences.
Calculate an n-period Smoothed Moving Average on the columns.
Divide the smoothed positive differences by the smoothed absolute negative differences. This is called the Relative Strength — RS.
Apply the below normalization formula to get the Relative Strength Index.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def adder(Data, times):
for i in range(1, times + 1):
new = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new, axis = 1)
return Data
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
def jump(Data, jump):
Data = Data[jump:, ]
return Data
def ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Data
def ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Data
def rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)
return Datamy_data = rsi(my_data, 21, 3, 4, width = 1, genre = 'Smoothed')Strategy Discussion: Oversold/Overbought Technique
The most common strategy used on the RSI is mean-reversion where the trader is supposed to detect extremes in momentum that signal a reversal.
An oversold level is a threshold in the Relative Strength Index where the market is perceived to be oversold and ready for a bullish reaction. The idea is that too much selling has happened and the market should recover briefly.
An overbought level is a threshold in the Relative Strength Index where the market is perceived to be overbought and ready for a bearish reaction. The idea is that too much buying has happened and the market should pause briefly.
To code a function that gives out signals of overselling and overbuying, the below code can be written:
lookback = 21
upper_barrier = 80
lower_barrier = 20
def signal(Data, rsi_col, buy, sell):
for i in range(len(Data)):
if Data[i, rsi_col] < lower_barrier and Data[i - 1, buy] == 0 and Data[i - 2, buy] == 0 and Data[i - 3, buy] == 0 and Data[i - 4, buy] == 0:
Data[i, buy] = 1
elif Data[i, rsi_col] > upper_barrier and Data[i - 1, sell] == 0 and Data[i - 2, sell] == 0 and Data[i - 3, sell] == 0 and Data[i - 4, sell] == 0:
Data[i, sell] = -1
return DataStrategy Discussion: Divergence Technique
Naturally, when prices are rising and making new tops while a price-based indicator is making lower tops, a weakening is occurring and a possibility to change the bias from long to short can present itself. That is what we call a normal divergence. We know that:
When prices are making higher highs while the indicator is making lower highs, it is called a bearish divergence, and the market might stall.
When prices are making lower lows while the indicator is making higher lows, it is called a bullish divergence, and the market might show some upside potential.
The above plot shows the EURUSD in the first panel with the 21-period RSI in the second panel. The bearish divergences are colored in red where we should expect some form of consolidation and the bullish divergences are colored in blue where we should expect some form of upside reaction.
A divergence is preferably considered when the indicator is around extremes. Notice how in the above example, the RSI readings are closer to 70 or 30 when we do detect the divergences. However, we can also consider 60 or 40 as extremes.
def divergence(Data, indicator, lower_barrier, upper_barrier, width, buy, sell):
for i in range(len(Data)):
try:
if Data[i, indicator] < lower_barrier:
for a in range(i + 1, i + width):
# First trough
if Data[a, indicator] > lower_barrier:
for r in range(a + 1, a + width):
if Data[r, indicator] < lower_barrier and Data[r, indicator] > Data[i, indicator] and Data[r, 3] < Data[i, 3]:
for s in range(r + 1, r + width):
# Second trough
if Data[s, indicator] > lower_barrier:
Data[s, buy] = 1
break
else:
break
else:
break
else:
break
else:
break
except IndexError:
pass
for i in range(len(Data)):
try:
if Data[i, indicator] > upper_barrier:
for a in range(i + 1, i + width):
# First trough
if Data[a, indicator] < upper_barrier:
for r in range(a + 1, a + width):
if Data[r, indicator] > upper_barrier and Data[r, indicator] < Data[i, indicator] and Data[r, 3] > Data[i, 3]:
for s in range(r + 1, r + width):
# Second trough
if Data[s, indicator] < upper_barrier:
Data[s, sell] = -1
break
else:
break
else:
break
else:
break
else:
break
except IndexError:
pass
return DataStrategy Discussion: Duration Technique
I have presented the RSI first because the Extreme Duration is simply an add-on to any bounded indicator. It is not an indicator on its own per se, but simply a way to see how long the indicator spends being overbought or oversold. We understand that:
An overbought Indicator is saying that the bullish momentum should fade soon and we might see a correction or even a reversal on the downside.
An oversold Indicator is saying that the bearish momentum should fade soon and we might see a correction or even a reversal on the upside.
However, if things were so simple, we would all be millionnaires. With this being said, let us take a look at the Extreme Duration below (calculated on the values of the RSI) before seeing how to code and analyze it.
The above plot shows the Extreme Duration calculation based on a 5-period RSI with barriers at 70 and 30. When the Extreme Duration is showing a reading of 5, it means that the 5-period RSI is above 70 for the fifth consecutive time (i.e. surpassed 70 and stayed above it for 5 units of time). We are used to analyze these indicators value-wise, we want to analyze them now time-wise.
To calculate the Extreme Duration, we can follow the below steps:
# Calculate the RSI on OHLC array (composed of 4 columns)
my_data= rsi(my_data, lookback, 3, 4, genre = 'Smoothed')
# Add a few spare columns to be populated with whatever you want
my_data = adder(my_data, 20)
# Define the Barriers (Oversold and Overbought zones)
upper_barrier = 70
lower_barrier = 30
# Define the Extreme Duration
def extreme_duration(Data, indicator, upper_barrier, lower_barrier, where_upward_extreme, where_downward_extreme):
# Time Spent Overbought
for i in range(len(Data)):
if Data[i, indicator] > upper_barrier:
Data[i, where_upward_extreme] = Data[i - 1, where_upward_extreme] + 1
else:
a = 0
Data[i, where_upward_extreme] = a
# Time Spent Oversold
for i in range(len(Data)):
if Data[i, indicator] < lower_barrier:
Data[i, where_downward_extreme] = Data[i - 1, where_downward_extreme] + 1
else:
a = 0
Data[i, where_downward_extreme] = a
Data[:, where_downward_extreme] = -1 * Data[:, where_downward_extreme]
return Data
# Calculating the Extreme Duration
my_data = extreme_duration(my_data, 4, upper_barrier, lower_barrier, 5, 6)Let us now try to use the Extreme Duration to generate signals based on this hypothesis:
“What if the average time spent on the extremes can help us understand when the indicator will exist these mentioned extremes?”
Based on a historical analysis, the average duration of the 5-period RSI is between 3 and 4. However, based on visual historical representation, it is closer to 5. Let us set the time barriers to 5 and -5.
The above plot shows the signals generated when the 5-period RSI on the EURUSD hourly data remains for at least 5 periods on the extremes.
def signal(Data, upward_timing, downward_timing, buy, sell):
for i in range(len(Data)):
if Data[i, downward_timing] <= -5 and Data[i - 1, downward_timing] >= -5 and Data[i - 2, downward_timing] >= -5:
Data[i, buy] = 1
if Data[i, upward_timing] >= 5 and Data[i - 1, upward_timing] <= 5 and Data[i - 2, upward_timing] <= 5 :
Data[i, sell] = -1A lot of optimization can be done on this promising technique, especially that only value-wise readings are not sufficient anymore. Temporal analysis is paramount to better understand how the underlying reacts.
Other Variations: The Simple Relative Strength Index
The Simple RSI is a simple change in the way the moving average is calculated inside the formula of the standard RSI. Instead of using a smoothed moving average as recommended by Wilder, we will use a simple moving average. Therefore, in the function provided above, we already have the choice and hence, we can write directly the following code:
my_data = rsi(my_data, 14, 3, 4, genre = 'Simple')
# The 14 refers to the lookback period on the RSI
# The 3 refers to the closing prices on the OHLC array
# The 4 refers to the index of the column where the RSI will be putIf you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
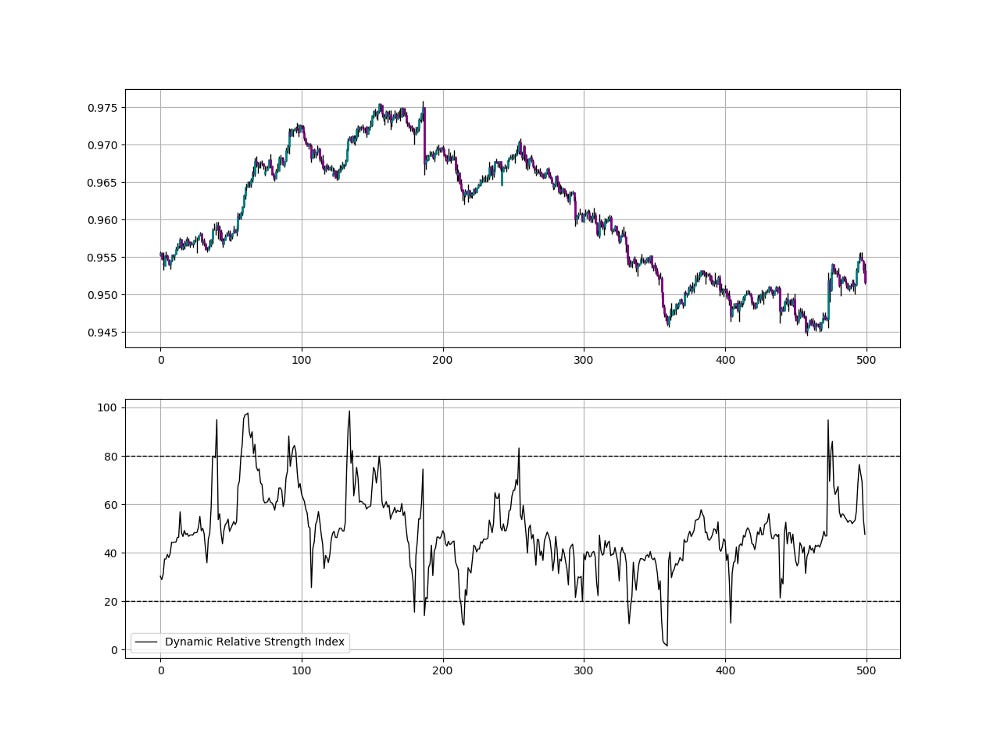
Other Variations: The Dynamic Relative Strength Index
Our first step into calculating the Dynamic Relative Strength Index is to calculate the Relative Volatility Index. Volatility is the magnitude of fluctuations of a variable around its mean. In time series, a volatile data is one that moves swiftly from one level to another and is generally away from its mean while a stable or low-volatility data is one that looks closer to its moving average (mean).
There are many ways to measure volatility such as the Average True Range, the Mean Absolute Deviation, and the Standard Deviation. We will use Standard Deviation to create the Relative Volatility Index.
The most basic type of volatility is the Standard Deviation. It is one of the pillars of descriptive statistics and an important element in some technical indicators such as the famous Bollinger Bands. But first let us define what Variance is before we find the Standard Deviation.
Variance is the squared deviations from the mean (a dispersion measure), we take the square deviations so as to force the distance from the mean to be non-negative, finally we take the square root to make the measure have the same units as the mean, in a way we are comparing apples to apples (mean to standard deviation standard deviation). Variance is calculated through this formula:
Following what we have said, standard deviation is therefore:
def volatility(Data, lookback, what, where):
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, what].std()) except IndexError:
pass
return DataThe exciting job now is to turn the historical volatility otherwise known as the historical Standard Deviation into an understandable indicator that resembles the Relative Strength Index. The below plot shows the Relative Volatility Index which is simply the RSI applied to 10-period standard deviation of the closing prices.
The idea of the Dynamic Relative Strength Index is to select the lookback period based on the recent volatility following this intuition:
Whenever the volatility is high according to the current Relative Volatility Index, we need to bias the lookback period on the Relative Strength Index downwards to account more for the recent values.
Whenever the volatility is low according to the current Relative Volatility Index, we need to bias the lookback period on the Relative Strength Index upwards to account less for the recent values.
Therefore, the two main components of the Dynamic Relative Strength Index are:
The Relative Volatility Index.
The Relative Strength Index.
How are we going to calculate this and how does it use volatility? It is a very simple concept, let us take a look at the below code:
def relative_volatility_index(Data, lookback, close, where):
# Calculating Volatility
Data = volatility(Data, lookback, close, where)
# Calculating the RSI on Volatility
Data = rsi(Data, lookback, where, where + 1, width = 1, genre = 'Smoothed')
# Cleaning
Data = deleter(Data, where, 1)
return Data
lookback = 10
def dynamic_relative_strength_index(Data, lookback, close, where):
# Calculating the Relative Volatility Index
Data = relative_volatility_index(Data, lookback, close, where)
# Adding a column
Data = adder(Data, 1)
# Calculating the Lookback Periods on the Dynamic Relative Strength Index
for i in range(len(Data)):
if Data[i, where] >= 0 and Data[i, where] <= 10 :
Data[i, where + 1] = 144
if Data[i, where] > 10 and Data[i, where] <= 20 :
Data[i, where + 1] = 89
if Data[i, where] > 20 and Data[i, where] <= 30 :
Data[i, where + 1] = 55
if Data[i, where] > 30 and Data[i, where] <= 40 :
Data[i, where + 1] = 34
if Data[i, where] > 40 and Data[i, where] <= 50 :
Data[i, where + 1] = 21
if Data[i, where] > 50 and Data[i, where] <= 60 :
Data[i, where + 1] = 13
if Data[i, where] > 60 and Data[i, where] <= 70 :
Data[i, where + 1] = 8
if Data[i, where] > 70 and Data[i, where] <= 80 :
Data[i, where + 1] = 5
if Data[i, where] > 80 and Data[i, where] <= 90 :
Data[i, where + 1] = 3
if Data[i, where] > 90 and Data[i, where] <= 100 :
Data[i, where + 1] = 2
# Calculating the Relative Strength Index
Data = rsi(Data, 2, close, where + 2)
Data = rsi(Data, 3, close, where + 3)
Data = rsi(Data, 5, close, where + 4)
Data = rsi(Data, 8, close, where + 5)
Data = rsi(Data, 13, close, where + 6)
Data = rsi(Data, 21, close, where + 7)
Data = rsi(Data, 34, close, where + 8)
Data = rsi(Data, 55, close, where + 9)
Data = rsi(Data, 89, close, where + 10)
Data = rsi(Data, 144, close, where + 11)
# Adding a column
Data = adder(Data, 1)
# Dynamic Relative Strength Index
for i in range(len(Data)):
if Data[i, where + 1] == 2:
Data[i, where + 12] = Data[i, where + 2]
if Data[i, where + 1] == 3:
Data[i, where + 12] = Data[i, where + 3] if Data[i, where + 1] == 5:
Data[i, where + 12] = Data[i, where + 4] if Data[i, where + 1] == 8:
Data[i, where + 12] = Data[i, where + 5] if Data[i, where + 1] == 13:
Data[i, where + 12] = Data[i, where + 6] if Data[i, where + 1] == 21:
Data[i, where + 12] = Data[i, where + 7] if Data[i, where + 1] == 34:
Data[i, where + 12] = Data[i, where + 8] if Data[i, where + 1] == 55:
Data[i, where + 12] = Data[i, where + 9] if Data[i, where + 1] == 89:
Data[i, where + 12] = Data[i, where + 10] if Data[i, where + 1] == 144:
Data[i, where + 12] = Data[i, where + 11]
# Cleaning
Data = deleter(Data, where, 12)
return DataWhat the above code simply does is calculate the 10-period Relative Volatility Index, then calculates an array of RSI’s on the market price using the following lookback periods {2, 3, 5, 8, 13, 21, 34, 55, 89, 144} which is simply the Fibonacci sequence (Big fan). Then the code will loop around the data and segment the Relative Volatility Index into 10 parts with each part assigned a Fibonacci period. For example:
If the Relative Volatility Index is showing a reading of 8, then it falls into the first part. With such low volatility, the lookback calculated on the RSI is 144. This is to account for the low current volatility.
If the Relative Volatility Index is showing a reading of 85, then it falls into the ninth part. With such high volatility, the lookback calculated on the RSI is 89. This is to account for the high current volatility.
The Dynamic Relative Strength Index witnesses from time to time spikes and this due to the change in volatility. It takes into account the current market properties and is therefore better at detecting short-term and long-term opportunities and signals. Unlike the normal RSI, the Dynamic RSI, when around 50, does not mean we are far from a signal due to the fact that it can spike at any time.
Other Variations: The RSI-Delta Indicator
The transformation is used to detect where the RSI is about to reverse knowing its extremely strong correlation with the market price. Technically, the RSI is already stationary and seems to reverse sooner or later when it hits the upper boundaries but that does not always coincide with price reversals. We need a more short-term way of seeking reversals and this is where we will subtract current RSI values from the ones preceding it.
The RSI Delta transformation provides an even more mean-reverting indicator as shown below in the chart.
Let us now calculate the correlation between the RSI Delta and the market price to see whether it is still strong or not.
correlation = 0.51 # For the last 80 observations which is goodConclusion & Important Disclaimer
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing Back-testing results should lead the reader to explore more herself the strategy and work on it more. That way you can share with me your better strategy and we will get rich together.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.