The Volatility-Adjusted RSI — A Modified Momentum Indicator.
Creating the Volatility-Adjusted Relative Strength Index in Python.
The Relative Strength Index is generally the most used bounded technical indicator. There are many strategies that can be formed around it and while not all of them seem to add direct value to profitability or at least they lack enough evidence to prove their usefulness, it should not stop us from thinking about new ways to exploit this simple yet wonderful tool that is the RSI.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a Github page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on Linkedin.
The Book of Trading Strategies
Amazon.com: The Book of Trading Strategies: 9798532885707: Kaabar, Sofien: Bookswww.amazon.com
The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def adder(Data, times):
for i in range(1, times + 1):
new = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new, axis = 1)
return Data
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
def jump(Data, jump):
Data = Data[jump:, ]
return Data
def ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Data
def rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)
return DataThe Relative Strength Index is known for the extremes strategy (Oversold and Overbought levels) where we initiate contrarian positions when the RSI is close to the extremes in an attempt to fade the current trend.
The Volatility-Adjusted Relative Strength Index
The RSI is calculated using closing prices. This has the small flaw in that it fails to account for the highs and lows made in the time period covered. A normal RSI will take into account the current closing price relative to the ones preceding it but will not exploit the information that is contained in the highs and lows. Now, the idea of integrating them may not add value at all but it should not stop us from exploring the concept.
Here are the original steps used to calculate the standard RSI as described by Welles Wilder, the father of many technical indicators:
Take the absolute difference between the closing price and the one before it.
Separate the upward differences from the downward differences.
Calculate the smoothed moving average on each of the differences using a specified lookback period (Usually 14 periods).
Divide the smoothed upward differences by the smoothed downward differences. This gives us the Relative Strength.
Use the below formula to normalize the Relative Strength between 0 and 100.
Now, what we can do to include the highs and lows are some simple modifications as shown in the following list:
Take the absolute difference between the high and the high before it.
Separate the upward differences from the downward differences.
Calculate the simple moving average on each of the differences using a specified lookback period (I prefer 13 periods as opposed to the usual 14 but there is no big difference).
Divide the averaged upward differences by the averaged downward differences. This gives us the Relative Strength.
Use the formula to normalize the Relative Strength between 0 and 100.
Now, Take the absolute difference between the low and the low before it.
Separate the upward differences from the downward differences.
Calculate the simple moving average on each of the differences using a specified lookback period (I prefer 13 periods as opposed to the usual 14 but there is no big difference).
Divide the averaged upward differences by the averaged downward differences. This gives us the Relative Strength.
Use the formula to normalize the Relative Strength between 0 and 100.
Calculate the average between the RSI of the Highs and the RSI of the lows in a separate column.
Now, to calculate the volatility-adjusted RSI, we have to apply the following conditions knowing that we have three separate columns each containing the RSI of the highs, the RSI of the lows, and the average between them:
If the RSI high is above 80, the value we retain is the RSI high.
If the RSI low is below 20, the value we retain is the RSI low.
If the average between the two is between 80 and 20, we retain its value.
def volatility_adjusted_rsi(Data, high, low, lookback, where):
# Adding Columns
Data = adder(Data, 20)
''' RSI HIGH EXTREME '''
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, high] - Data[i - 1, high]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
''' RSI LOW EXTREME '''
# Calculating Differences
where = where + 1
for i in range(len(Data)):
Data[i, where] = Data[i, low] - Data[i - 1, low]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
''' RSI VOLATILITY-ADJUSTED '''
where = where + 1
# Averaging
Data[:, where] = (Data[:, where - 2] + Data[:, where - 1]) / 2
# Conditions
for i in range(len(Data)):
if Data[i, where - 2] > upper_barrier:
Data[i, where + 1] = Data[i, where - 2]
elif Data[i, where - 1] < lower_barrier:
Data[i, where + 1] = Data[i, where - 1]
elif Data[i, where - 2] < upper_barrier and Data[i, where - 1] > lower_barrier:
Data[i, where + 1] = Data[i, where]
# Cleaning
Data = deleter(Data, where - 2, 3)
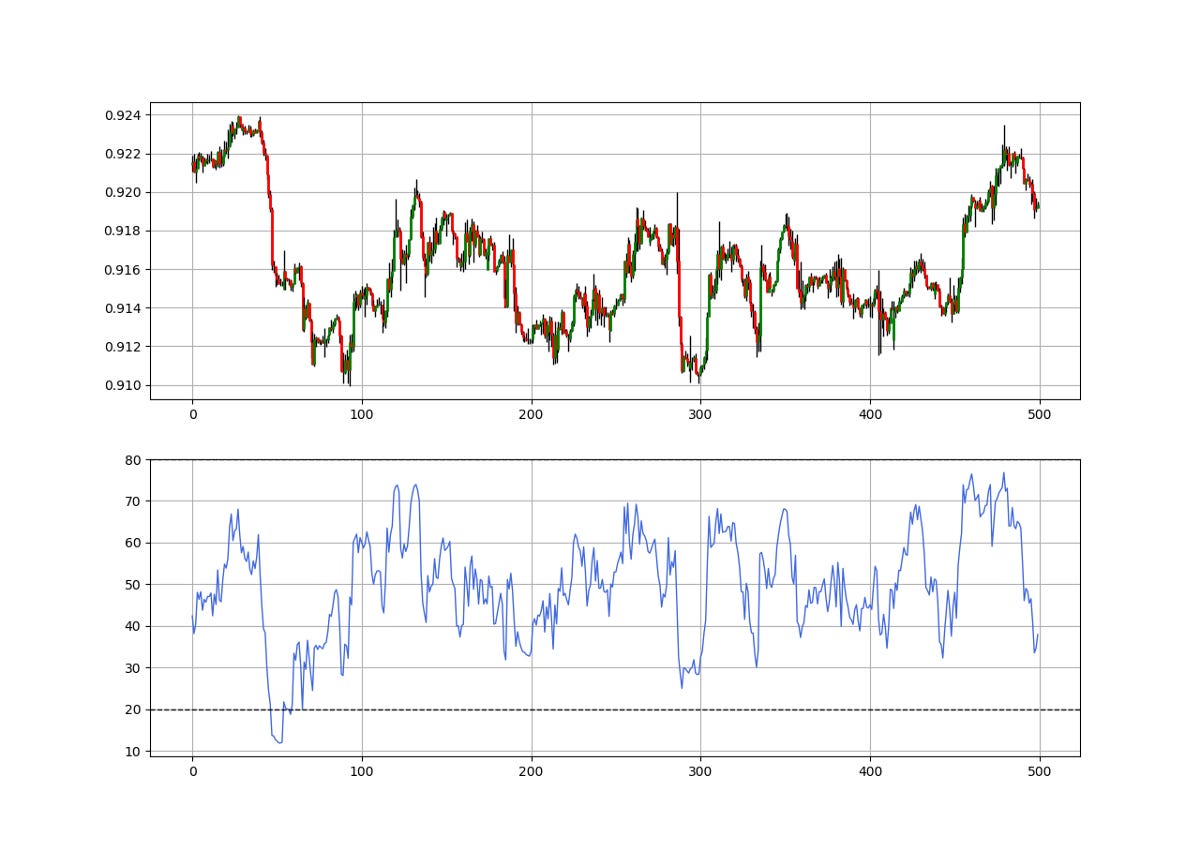
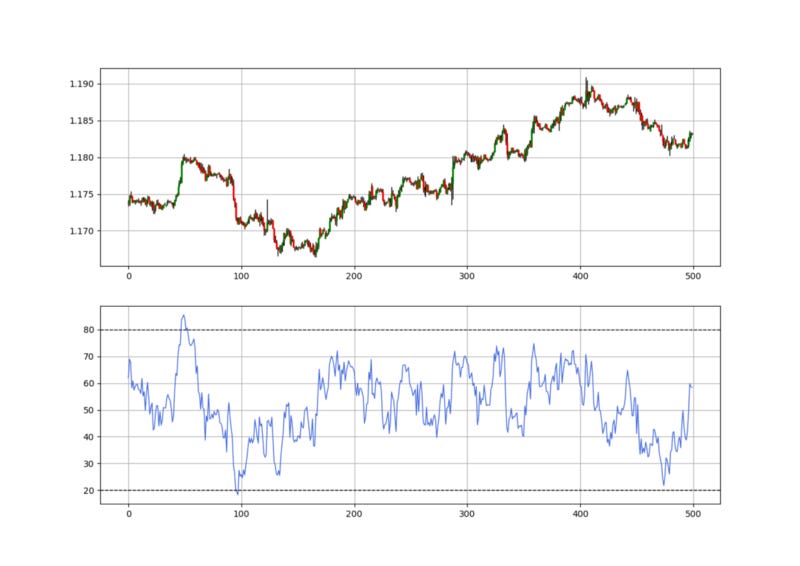
return DataThe below chart shows the difference between a normal RSI and a volatility-adjusted RSI. We can see that it is much more responsive to volatility where it is incorporated so that we get more signals missed out by the regular RSI.
In essence, the volatility-adjusted RSI is simply more reactive, but this in no way means that it is superior than the good old RSI we know. A lot of tweaking and optimization is possible to reach a stable strategy.
Using the Volatility-Adjusted Relative Strength Index
The new indicator is used exactly as the normal one. These are some slight differences to account for:
The divergence strategy: With the normal RSI we need to account for divergences using only closing prices while with the volatility-adjusted RSI we can include the highs and lows of the market price when detecting divergences.
The oversold/overbought strategy may work differently with the volatility-adjusted RSI. We can use the integration strategy instead. This strategy initiates the signals when the RSI exits the extreme reading.
However, for comparability reasons, let us back-test the simple oversold/overbought strategy with the same conditions but one using the regular 13-period RSI and the other using the 13-period volatility-adjusted RSI.
A buy (Long) signal is generated whenever the RSI breaks the 20 level.
A sell (Short) signal is generated whenever the RSI surpasses the 80 level.
def signal(Data, what, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, what] <= lower_barrier and Data[i - 1, buy] == 0 and Data[i - 2, buy] == 0 and Data[i - 3, buy] == 0 and Data[i - 1, what] > lower_barrier:
Data[i, buy] = 1
elif Data[i, what] >= upper_barrier and Data[i - 1, sell] == 0 and Data[i - 2, sell] == 0 and Data[i - 3, sell] == 0 and Data[i - 1, what] < upper_barrier:
Data[i, sell] = -1
return DataHaving had the signals, we now know when the algorithm would have placed its buy and sell orders, meaning, that we have an approximate replica of the past where can can control our decisions with no hindsight bias. We have to simulate how the strategy would have done given our conditions. This means that we need to calculate the returns and analyze the performance metrics. Let us see a neutral metric that can give us somewhat a clue on the predictability of the indicator or the strategy. For this study, we will use the Signal Quality metric.
The signal quality is a metric that resembles a fixed holding period strategy. It is simply the reaction of the market after a specified time period following the signal. Generally, when trading, we tend to use a variable period where we open the positions and close out when we get a signal on the other direction or when we get stopped out (either positively or negatively).
Sometimes, we close out at random time periods. Therefore, the signal quality is a very simple measure that assumes a fixed holding period and then checks the market level at that time point to compare it with the entry level. In other words, it measures market timing by checking the reaction of the market.
# Choosing the holding period
period = 1
def signal_quality(Data, closing, buy, sell, period, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
if Data[i, buy] == 1:
Data[i + period, where] = Data[i + period, closing] - Data[i, closing]
if Data[i, sell] == -1:
Data[i + period, where] = Data[i, closing] - Data[i + period, closing]
except IndexError:
pass
return Data
# Applying the Signal Quality Function
my_data = signal_quality(my_data, 3, 6, 7, period, 8)
positives = my_data[my_data[:, 8] > 0]
negatives = my_data[my_data[:, 8] < 0]
# Calculating Signal Quality
signal_quality = len(positives) / (len(negatives) + len(positives))
print('Signal Quality = ', round(signal_quality * 100, 2), '%')
# Output Regular RSI = 54.05% on the hourly EURUSD
# Output Volatility-Adjusted RSI = 54.70% on the hourly EURUSDAs an example of a neutral back-testing measure based on the closing price right after the signal, we can find that the volatility-adjusted RSI outperforms the regular RSI when it comes to the hourly values of the EURUSD since 2011.
If you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
New Technical Indicators in Python
Amazon.com: New Technical Indicators in Python: 9798711128861: Kaabar, Mr Sofien: Bookswww.amazon.com
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.









Thats really good, I am making so many new indicators from previous SMA based RSI post , cant wait to try this out!