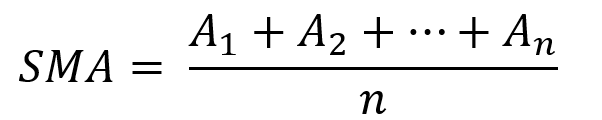The Volatility-Adjusted Moving Average. New Trend-Following Horizons.
Coding the Volatility-Adjusted Moving Average in Python.
Adjusting for volatility is a powerful technique to account for the recent price action. Most moving averages fail to do so and thus they miss a part of the picture. Surely they are useful in their own but every moving average has its own flaws. This article discusses and presents a type of moving average that accounts for volatility.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Concept of Moving Averages
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data filedef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return DataAs the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
The below states that the moving average function will be called on the array named my_data for a lookback period of 200, on the column indexed at 3 (closing prices in an OHLC array). The moving average values will then be put in the column indexed at 4 which is the one we have added using the adder function.
my_data = ma(my_data, 200, 3, 4)The Concept of Volatility
We must first understand the concept of Volatility. It is a key concept in finance, whoever masters it holds a tremendous edge in the markets.
Unfortunately, we cannot always measure and predict it with accuracy. Even though the concept is more important in options trading, we need it pretty much everywhere else. Traders cannot trade without volatility nor manage their positions and risk. Quantitative analysts and risk managers require volatility to be able to do their work. Before we discuss the different types of volatility, why not look at a graph that sums up the concept? Check out the below image to get you started.
You can code the above in Python yourself using the following snippet:
# Importing the necessary libraries
import numpy as np
import matplotlib.pyplot as plt# Creating high volatility noise
hv_noise = np.random.normal(0, 1, 250)# Creating low volatility noise
lv_noise = np.random.normal(0, 0.1, 250)# Plotting
plt.plot(hv_noise, color = 'red', linewidth = 1.5, label = 'High Volatility')plt.plot(lv_noise, color = 'green', linewidth = 1.5, label = 'Low Volatility')plt.axhline(y = 0, color = 'black', linewidth = 1)plt.grid()
plt.legend()The different types of volatility around us can be summed up in the following:
Historical volatility: It is the realized volatility over a certain period of time. Even though it is backward looking, historical volatility is used more often than not as an expectation of future volatility. One example of a historical measure is the standard deviation, which we will use for the volatility-adjusted moving average.
Implied volatility: In its simplest definition, implied volatility is the measure that when inputted into the Black-Scholes equation, gives out the option’s market price. It is considered as the expected future actual volatility by market participants. It has one time scale, the option’s expiration.
Forward volatility: It is the volatility over a specific period in the future.
Actual volatility: It is the amount of volatility at any given time. Also known as local volatility, this measure is hard to calculate and has no time scale.
The most basic type of volatility is our old friend “the Standard Deviation”. It is one of the pillars of descriptive statistics and an important element in some technical indicators (such as the Bollinger Bands). But first let us define what variance is before we find Standard Deviation.
Variance is the squared deviations from the mean (a dispersion measure), we take the square deviations so as to force the distance from the mean to be non-negative, finally we take the square root to make the measure have the same units as the mean, in a way we are comparing apples to apples (mean to standard deviation standard deviation). Variance is calculated through this formula:
Following our logic, standard deviation is therefore:
Therefore, if we want to understand the concept in layman’s terms, we can say that Standard Deviation is the average distance away from the mean that we expect to find when we analyze the different components of the time series.
Now, let us code a function that calculates a rolling standard deviation of a certain time series.
def volatility(Data, lookback, what, where):
# Adding an extra column
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, what].std())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return DataIf you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Creating the Volatility-Adjusted Moving Average
The volatility-adjusted moving average — VAMA — is a technical indicator created by Tushar S. Chande. Commonly referred to as the Variable Index Moving Average, it is a powerful indicator that uses two standard deviation periods to account for recent volatility. I have taken the liberty to rename it into the volatility-adjusted moving average because there is a newer version with the same name that uses the Chande momentum oscillator instead of the standard deviation, hence it is important to distinguish the difference between the two.
The first step to calculate the VAMA is to measure the alpha which can be found through this formula below:
Therefore, the alpha is calculated as a ratio between a short-term volatility calculation and a long-term volatility calculation. The result is multiplied by 0.20. Then, to calculate the VAMA, we follow these steps.
The first VAMA value is simply the closing price, and then the algorithm can take the form of the above formula.
The above chart shows the GBPUSD hourly values with the VAMA using a 3-period standard deviation and a 144-period standard deviation. To code the VAMA, we use the below function
def volatility_adjusted_moving_average(Data, lookback_volatility_short, lookback_volatility_long, close, where):
# Adding Columns
Data = adder(Data, 2)
# Calculating Standard Deviations
Data = volatility(Data, lookback_volatility_short, close, where)
Data = volatility(Data, lookback_volatility_long, close, where + 1)
# Calculating Alpha
for i in range(len(Data)):
Data[i, where + 2] = 0.2 * (Data[i, where] / Data[i, where + 1])
# Calculating the First Value of VAMA
Data[1, where + 3] = (Data[1, where + 2] * Data[1, close]) + ((1 - Data[1, where + 2]) * Data[0, close])
# Calculating the Rest of VAMA
for i in range(2, len(Data)):
Data[i, where + 3] = (Data[i, where + 2] * Data[i, close]) + ((1 - Data[i, where + 2]) * Data[i - 1, where + 3]) # Cleaning
Data = deleter(Data, where, 3)
Data = jump(Data, 1)
return Datalookback_volatility_short = 3
lookback_volatility_long = 144my_data = volatility_adjusted_moving_average(my_data, lookback_volatility_short, lookback_volatility_long, 3, 4)The way to use the VAMA is to follow the trend with it or simply expect reactions from it whenever the market approaches it. There are a lot of combinations to be made with this moving average, so be creative!
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.