Machine learning for time series is an ever-evolving field where new techniques and methods are constantly discovered with the aim of improving the predictive ability of the models. This article presents three boosting algorithms known to have a high capacity of dealing with complex data.
✨ Important note
Boosting is a machine learning ensemble technique used to improve the predictive performance of a model by combining the predictions of multiple weaker models, typically called base or weak learners.
The basic idea behind boosting is to sequentially train a series of weak learners on different subsets of the training data, with each subsequent learner focusing more on the instances that were misclassified by the previous ones.
Quick Introduction to Decision Trees
Before understanding the boosting algorithms, it is imperative to have a basic knowledge of decision trees.
Decision trees are a fundamental tool in data analysis and machine learning that help in making decisions based on input data. Imagine you’re trying to decide whether to go for a picnic or not. Your decision might depend on various factors like weather, location, and availability of friends. Similarly, decision trees in data analysis help you make decisions by analyzing different variables and their outcomes.
At its core, a decision tree is like a flowchart where each internal node represents a decision based on a specific feature or attribute, each branch represents the outcome of that decision, and each leaf node represents the final decision or outcome. For instance, in our picnic example, the decision tree might start with the question “Is it raining?” If yes, it might lead to a decision not to go for a picnic; if no, it might further branch into questions about temperature or wind speed.
Decision trees are particularly useful because they’re easy to understand and interpret. You can visually trace the decision-making process, making it transparent and intuitive. They’re also versatile, capable of handling both numerical and categorical data, and they can easily handle interactions between variables.
One key aspect of decision trees is how they make decisions: by recursively splitting the data into subsets based on the most “informative” feature at each step. This process continues until the data in each branch is as “pure” as possible, meaning it contains mostly one class or outcome. This splitting process is guided by various algorithms like CART.
However, decision trees are prone to overfitting, meaning they can become too tailored to the training data and perform poorly on unseen data.
The following graph shows the function of a decision tree.
Overall, decision trees provide a powerful and intuitive way to make decisions based on data, making them a cornerstone of machine learning and data analysis.
We will now discuss three algorithms known as boosting algorithms, and then we will use them to predict time series. The three algorithms are:
AdaBoost algorithm.
XGBoost algorithm.
CatBoost agorithm.
AdaBoost Algorithm
AdaBoost, short for Adaptive Boosting, is a popular ensemble learning method used in machine learning for building a strong predictive model by combining multiple weak learners, typically decision trees or other simple models. It was introduced by Yoav Freund and Robert Schapire in 1996 and has since become one of the most widely used boosting algorithms.
The fundamental idea behind AdaBoost is to sequentially train a series of weak learners on different subsets of the training data and then combine their predictions to create a strong learner. In each iteration of the training process, AdaBoost assigns higher weights to the instances that were misclassified by the previous weak learners, thus focusing more on the difficult-to-classify instances. This adaptive learning approach allows AdaBoost to continuously improve its performance over successive iterations.
One of the key strengths of AdaBoost is its ability to handle both classification and regression tasks effectively. In classification problems, AdaBoost constructs a series of weak classifiers, each of which tries to classify the data correctly, and then combines their predictions using a weighted majority vote. In regression problems, AdaBoost similarly constructs a series of weak regression models and combines their predictions through a weighted average.
One of the reasons for AdaBoost’s popularity is its simplicity and ease of implementation. Unlike some other ensemble methods, AdaBoost does not require complex parameter tuning or feature engineering, making it accessible to practitioners with varying levels of expertise.
Let’s consider the following example (which will also be applied to the other two boosting algorithms):
Time series: The ISM PMI.
Training data: The first 70% of the data since the creation of the index.
Test data: The last 30% of the data.
Features: The last six changes in the index.
✨ Important note
The ISM PMI, or Institute for Supply Management’s Purchasing Managers’ Index, is an economic indicator used to gauge the health and direction of the manufacturing sector in the United States. It’s based on a monthly survey of purchasing managers from various industries, asking questions about factors such as new orders, production levels, employment, supplier deliveries, and inventories.
Use the following code to implement the experiment:
from sklearn.ensemble import AdaBoostRegressor
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data = np.reshape(pd.read_excel('ISM_PMI.xlsx').values, (-1))
data = np.diff(data)
def data_preprocessing(data, num_lags, train_test_split):
# Prepare the data for training
x = []
y = []
for i in range(len(data) - num_lags):
x.append(data[i:i + num_lags])
y.append(data[i+ num_lags])
# Convert the data to numpy arrays
x = np.array(x)
y = np.array(y)
# Split the data into training and testing sets
split_index = int(train_test_split * len(x))
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]
return x_train, y_train, x_test, y_test
x_train, y_train, x_test, y_test = data_preprocessing(data, 6, 0.70)
# Create the model
model = AdaBoostRegressor(random_state = 123)
# Fit the model to the data
model.fit(x_train, y_train)
y_pred_xgb = model.predict(x_test)
# Plotting
plt.plot(y_pred_xgb[-100:], label='Predicted Data', linestyle='--', marker = '.', color = 'orange')
plt.plot(y_test[-100:], label='True Data', marker = '.', alpha = 0.7, color = 'blue')
plt.legend()
plt.grid()
plt.axhline(y = 0, color = 'black', linestyle = '--')
same_sign_count = np.sum(np.sign(y_pred_xgb) == np.sign(y_test)) / len(y_test) * 100
print('Hit Ratio = ', same_sign_count, '%')Another important characteristic of AdaBoost is its resistance to overfitting. By focusing on the misclassified instances in each iteration, AdaBoost implicitly performs a form of regularization, which helps prevent the model from memorizing the training data and improves its generalization performance on unseen data.
However, AdaBoost is sensitive to noisy data and outliers, as it assigns higher weights to misclassified instances, which can potentially amplify the influence of outliers. Additionally, AdaBoost’s performance may degrade if the weak learners are too complex or if the dataset is highly imbalanced.
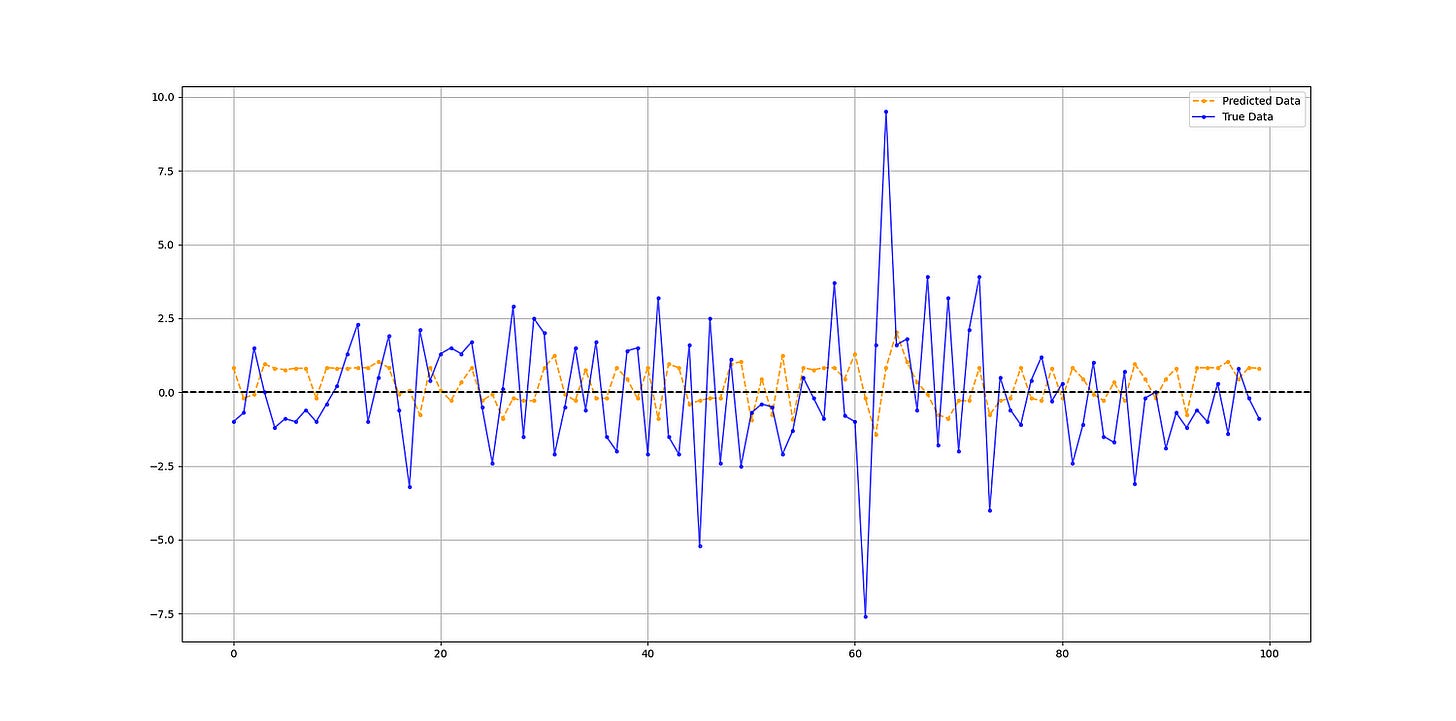
The output of the code is as follows:
Hit Ratio = 45.925925925925924 %XGBoost Algorithm
XGBoost, short for eXtreme Gradient Boosting, is an advanced implementation of gradient boosting algorithms. Gradient boosting is a popular technique used in machine learning for building predictive models. It’s based on the idea of combining multiple weak learners (often decision trees) sequentially, with each new learner focusing on the mistakes made by the previous ones.
XGBoost takes this concept to the next level by incorporating several optimizations and enhancements that make it one of the most powerful and efficient gradient boosting frameworks available today.
One of the key features of XGBoost is its focus on scalability and speed. It’s designed to handle large datasets efficiently, making it suitable for a wide range of applications, from industry-scale predictive modeling to academic research. XGBoost achieves this through parallelization and tree pruning techniques, which help speed up the training process significantly.
Another important aspect of XGBoost is its regularization techniques, which help prevent overfitting and improve generalization performance. Regularization is crucial in machine learning to ensure that the model doesn’t memorize the training data but instead learns patterns that can be generalized to unseen data. XGBoost achieves regularization through techniques like L1 and L2 regularization and tree complexity control.
Furthermore, XGBoost supports a wide range of customization options and hyperparameters, allowing users to fine-tune the model according to their specific requirements and the nature of their data. This flexibility makes XGBoost suitable for a variety of tasks, from classification and regression to ranking and recommendation systems.
XGBoost’s popularity and effectiveness have been demonstrated in various machine learning competitions and real-world applications, where it has consistently outperformed other algorithms and achieved state-of-the-art results. Its robustness, efficiency, and versatility make it a go-to choice for data scientists and machine learning practitioners worldwide.
Use the following code to implement the experiment:
from xgboost import XGBRegressor
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data = np.reshape(pd.read_excel('ISM_PMI.xlsx').values, (-1))
data = np.diff(data)
def data_preprocessing(data, num_lags, train_test_split):
# Prepare the data for training
x = []
y = []
for i in range(len(data) - num_lags):
x.append(data[i:i + num_lags])
y.append(data[i+ num_lags])
# Convert the data to numpy arrays
x = np.array(x)
y = np.array(y)
# Split the data into training and testing sets
split_index = int(train_test_split * len(x))
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]
return x_train, y_train, x_test, y_test
x_train, y_train, x_test, y_test = data_preprocessing(data, 6, 0.70)
# Create the model
model = XGBRegressor(random_state = 0, n_estimators = 32, max_depth = 32)
# Fit the model to the data
model.fit(x_train, y_train)
y_pred_xgb = model.predict(x_test)
# Plotting
plt.plot(y_pred_xgb[-100:], label='Predicted Data', linestyle='--', marker = '.', color = 'orange')
plt.plot(y_test[-100:], label='True Data', marker = '.', alpha = 0.7, color = 'blue')
plt.legend()
plt.grid()
plt.axhline(y = 0, color = 'black', linestyle = '--')
same_sign_count = np.sum(np.sign(y_pred_xgb) == np.sign(y_test)) / len(y_test) * 100
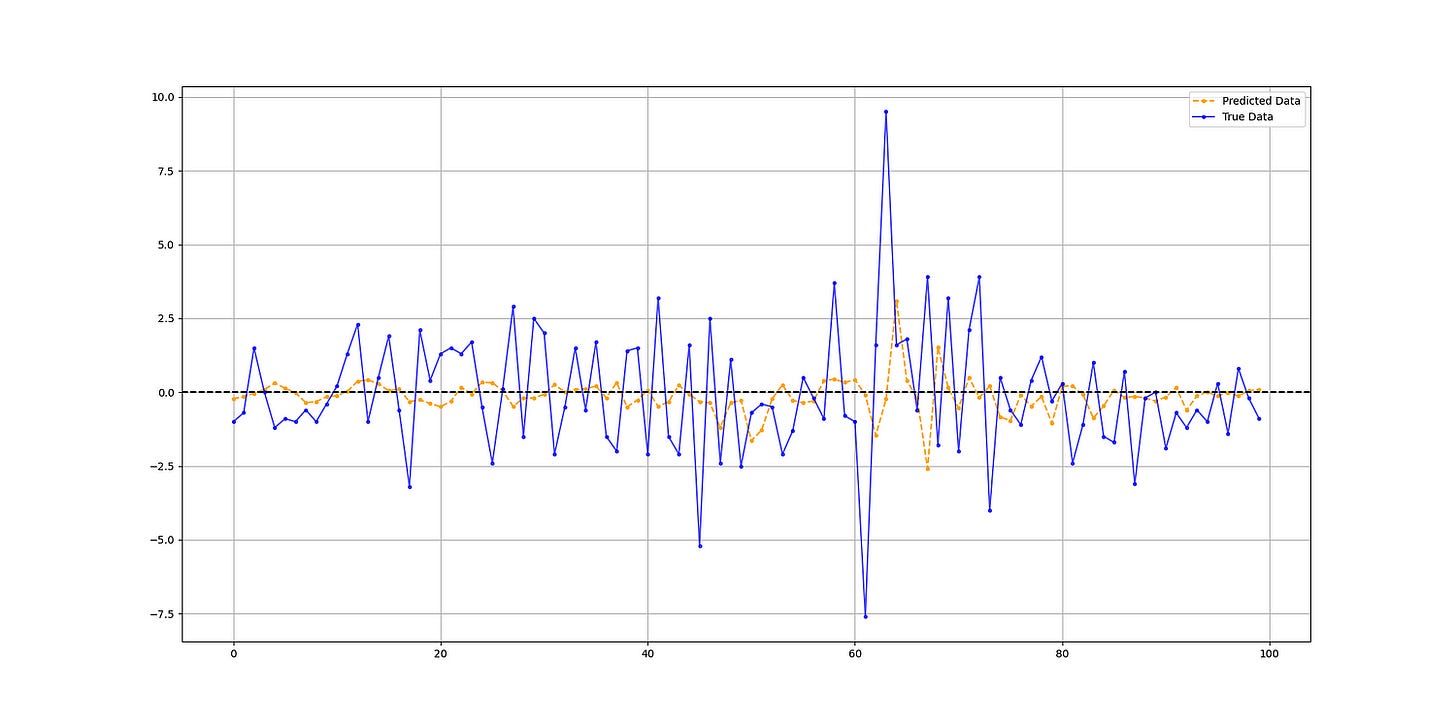
print('Hit Ratio = ', same_sign_count, '%')The output of the code is as follows:
Hit Ratio = 51.11111111111111 %CatBoost Algorithm
CatBoost is a high-performance gradient boosting library developed by Yandex, a Russian multinational corporation known for its web search engine. It’s specifically designed to tackle challenges in machine learning tasks involving categorical features, which are common in real-world datasets but can be difficult to handle with traditional gradient boosting algorithms.
✨ Important note
The name “CatBoost” is derived from its focus on categorical features (“Cat”) and its use of gradient boosting (“Boost”) techniques.
One of the key strengths of CatBoost lies in its ability to handle categorical features naturally and efficiently. Unlike many other gradient boosting implementations that require one-hot encoding or feature preprocessing for categorical variables, CatBoost can directly handle categorical features without the need for extensive preprocessing. This is achieved through an innovative algorithm that effectively handles categorical variables by considering their statistics during the tree building process.
CatBoost also incorporates several optimization techniques to improve training speed and performance. It utilizes an efficient implementation of gradient boosting with histogram-based splitting, which speeds up the training process by reducing the computational overhead associated with finding optimal split points for continuous features. Additionally, CatBoost employs a novel method for handling missing values, which allows it to seamlessly handle datasets with missing values without the need for imputation.
Another noteworthy feature of CatBoost is its built-in support for handling various types of data, including numerical, categorical, and text data. This versatility makes CatBoost well-suited for a wide range of machine learning tasks, from classification and regression to ranking and recommendation systems.
CatBoost also provides robustness against overfitting through built-in regularization techniques, such as depth regularization and learning rate shrinkage. These techniques help prevent the model from memorizing the training data and improve its generalization performance on unseen data.
Use the following code to implement the experiment:
from catboost import CatBoostRegressor
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
data = np.reshape(pd.read_excel('ISM_PMI.xlsx').values, (-1))
data = np.diff(data)
def data_preprocessing(data, num_lags, train_test_split):
# Prepare the data for training
x = []
y = []
for i in range(len(data) - num_lags):
x.append(data[i:i + num_lags])
y.append(data[i+ num_lags])
# Convert the data to numpy arrays
x = np.array(x)
y = np.array(y)
# Split the data into training and testing sets
split_index = int(train_test_split * len(x))
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]
return x_train, y_train, x_test, y_test
x_train, y_train, x_test, y_test = data_preprocessing(data, 6, 0.70)
# Create the model
model = CatBoostRegressor(iterations = 100, learning_rate = 0.1, depth = 6, loss_function = 'RMSE')
# Fit the model to the data
model.fit(x_train, y_train)
y_pred_xgb = model.predict(x_test)
# Plotting
plt.plot(y_pred_xgb[-100:], label='Predicted Data', linestyle='--', marker = '.', color = 'orange')
plt.plot(y_test[-100:], label='True Data', marker = '.', alpha = 0.7, color = 'blue')
plt.legend()
plt.grid()
plt.axhline(y = 0, color = 'black', linestyle = '--')
same_sign_count = np.sum(np.sign(y_pred_xgb) == np.sign(y_test)) / len(y_test) * 100
print('Hit Ratio = ', same_sign_count, '%')The output of the code is as follows:
Hit Ratio = 48.148148148148145 %Overall, the most important thing with algorithms is proper tuning and choosing the right features. Obviously, with these experiments, much work can be done to improve them.
You can also check out my other newsletter The Weekly Market Sentiment Report that sends weekly directional views every weekend to highlight the important trading opportunities using a mix between sentiment analysis (COT report, put-call ratio, etc.) and rules-based technical analysis.
If you liked this article, do not hesitate to like and comment, to further the discussion!