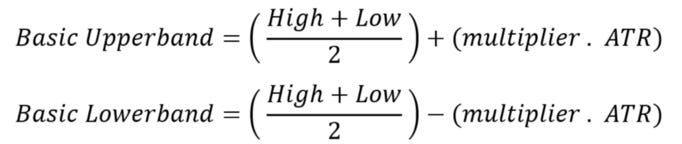The SuperTrend RSI Confirmation Strategy in Python
Creating a Powerful Strategy Based on the SuperTrend & the RSI
The RSI and the SuperTrend indicators are among the most powerful technical tools we have, therefore combining them can be lucrative. This article discusses one common strategy that relies on the two indicators.
Knowledge must be accessible to everyone. This is why, from now on, a purchase of either one of my new books “Contrarian Trading Strategies in Python” or “Trend Following Strategies in Python” comes with free PDF copies of my first three books (Therefore, purchasing one of the new books gets you 4 books in total). The two new books listed above feature a lot of advanced indicators and strategies with a GitHub page. You can use the below link to purchase one of the two books (Please specify which one and make sure to include your e-mail in the note).
Pay Kaabar using PayPal.Me
Go to paypal.me/sofienkaabar and type in the amount. Since it’s PayPal, it’s easy and secure. Don’t have a PayPal…www.paypal.com
The RSI
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def adder(Data, times):
for i in range(1, times + 1):
new = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new, axis = 1)
return Datadef deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Datadef jump(Data, jump):
Data = Data[jump:, ]
return Datadef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)
return DataCheck out my weekly market sentiment report to understand the current positioning and to estimate the future direction of several major markets through complex and simple models working side by side. Find out more about the report through this link that covers the analysis between 07/08/2022 and 14/08/2022:
Coalescence Report 7th August — 14th August 2022
THIS IS A FREE SAMPLE GIVEN TO FREE SUBSCRIBERS THIS WEEK. IF YOU WANT TO REGULARLY HAVE THIS REPORT, MAKE SURE TO…coalescence.substack.com
The SuperTrend Indicator
The first concept we should understand before creating the SuperTrend indicator is volatility. We sometimes measure volatility using the Average True Range. Although the ATR is considered a lagging indicator, it gives some insights as to where volatility is right now and where has it been last period (day, week, month, etc.). But before that, we should understand how the True Range is calculated (the ATR is just the average of that calculation).
The true range is simply the greatest of the three price differences:
High — Low
| High — Previous close |
| Previous close — Low |
Once we have gotten the maximum out of the above three, we simply take an average of n periods of the true ranges to get the Average True Range. Generally, since in periods of panic and price depreciation we see volatility go up, the ATR will most likely trend higher during these periods, similarly in times of steady uptrends or downtrends, the ATR will tend to go lower.
One should always remember that this indicator is lagging and therefore has to be used with extreme caution. Below is the function code that calculates the ATR. Make sure you have an OHLC array of historical data.
def adder(Data, times):
for i in range(1, times + 1):
new = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new, axis = 1)
return Datadef deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
def jump(Data, jump):
Data = Data[jump:, ]
return Datadef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef atr(Data, lookback, high, low, close, where, genre = 'Smoothed'):
# Adding the required columns
Data = adder(Data, 1)
# True Range Calculation
for i in range(len(Data)):
try:
Data[i, where] = max(Data[i, high] - Data[i, low],
abs(Data[i, high] - Data[i - 1, close]),
abs(Data[i, low] - Data[i - 1, close]))
except ValueError:
pass
Data[0, where] = 0
if genre == 'Smoothed':
# Average True Range Calculation
Data = ema(Data, 2, lookback, where, where + 1)
if genre == 'Simple':
# Average True Range Calculation
Data = ma(Data, lookback, where, where + 1)
# Cleaning
Data = deleter(Data, where, 1)
Data = jump(Data, lookback)
return DataNow that we have understood what the ATR is and how to calculate it, we can proceed further with the SuperTrend indicator. The indicator seeks to provide entry and exit levels for trend followers. You can think of it as a moving average or an MACD. Its uniqueness is its main advantage and although its calculation method is much more complicated than the other two indicators, it is intuitive in nature and not that hard to understand. Basically, we have two variables to choose from.
The ATR lookback and the multiplier’s value. The former is just the period used to calculated the ATR while the latter is generally an integer (usually 2 or 3).
The first thing to do is to average the high and low of the price bar, then we will either add or subtract the average with the selected multiplier multiplied by the ATR as shown in the above formulas. This will give us two arrays, the basic upper band and the basic lower band which form the first building blocks in the SuperTrend indicator. The next step is to calculate the final upper band and the final lower band using the below formulas.
It may seem complicated but most of these conditions are repetitive and in any case, I will provide the Python code below so that you can play with the function and optimize it to your trading preferences. Finally, using the previous two calculations, we can find the SuperTrend.
def supertrend(Data, multiplier, atr_col, close, high, low, where):
Data = adder(Data, 6)
for i in range(len(Data)):
# Average Price
Data[i, where] = (Data[i, high] + Data[i, low]) / 2
# Basic Upper Band
Data[i, where + 1] = Data[i, where] + (multiplier * Data[i, atr_col])
# Lower Upper Band
Data[i, where + 2] = Data[i, where] - (multiplier * Data[i, atr_col])
# Final Upper Band
for i in range(len(Data)):
if i == 0:
Data[i, where + 3] = 0
else:
if (Data[i, where + 1] < Data[i - 1, where + 3]) or (Data[i - 1, close] > Data[i - 1, where + 3]):
Data[i, where + 3] = Data[i, where + 1]
else:
Data[i, where + 3] = Data[i - 1, where + 3]
# Final Lower Band
for i in range(len(Data)):
if i == 0:
Data[i, where + 4] = 0
else:
if (Data[i, where + 2] > Data[i - 1, where + 4]) or (Data[i - 1, close] < Data[i - 1, where + 4]):
Data[i, where + 4] = Data[i, where + 2]
else:
Data[i, where + 4] = Data[i - 1, where + 4]
# SuperTrend
for i in range(len(Data)):
if i == 0:
Data[i, where + 5] = 0
elif (Data[i - 1, where + 5] == Data[i - 1, where + 3]) and (Data[i, close] <= Data[i, where + 3]):
Data[i, where + 5] = Data[i, where + 3]
elif (Data[i - 1, where + 5] == Data[i - 1, where + 3]) and (Data[i, close] > Data[i, where + 3]):
Data[i, where + 5] = Data[i, where + 4]
elif (Data[i - 1, where + 5] == Data[i - 1, where + 4]) and (Data[i, close] >= Data[i, where + 4]):
Data[i, where + 5] = Data[i, where + 4]
elif (Data[i - 1, where + 5] == Data[i - 1, where + 4]) and (Data[i, close] < Data[i, where + 4]):
Data[i, where + 5] = Data[i, where + 3]
# Cleaning columns
Data = deleter(Data, where, 5)
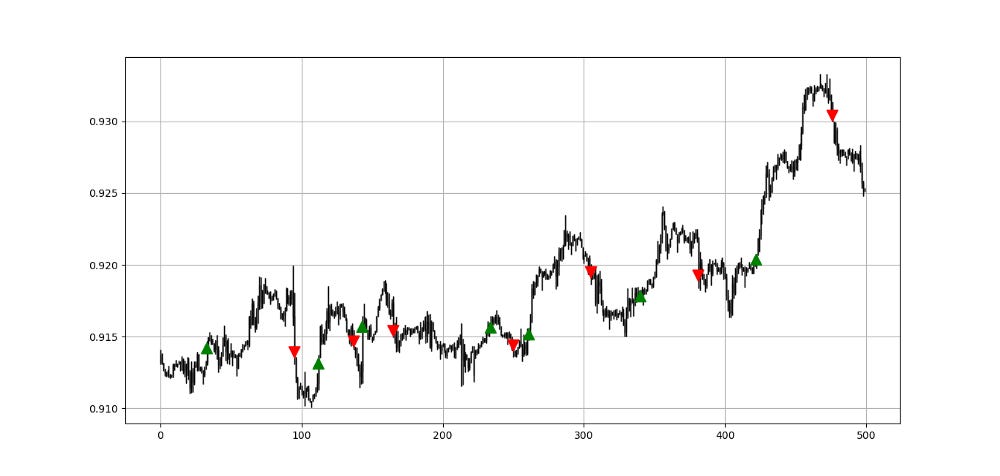
return DataThe above chart shows the hourly values of the EURUSD with a 10-period SuperTrend (represented by the ATR period) and a multiplier of 1.25.
The way we should understand the indicator is that when it goes above the market price, we should be looking to short and when it goes below the market price, we should be looking to go long as we anticipate a bullish trend. Remember that the SuperTrend is a trend-following indicator. The aim here is to capture trends at the beginning and to close out when they are over.
Creating & Evaluating the Strategy
Now, our job is to have an array that contains the OHLC data, alongside the columns for the RSI and the SuperTrend. We can do that by following this code granted we have imported the necessary historical data.
# Indicator Parameters
lookback_rsi = 13
lookback_supertrend = 10
multiplier = 3# Adding a few columns
my_data = adder(my_data, 10)# Calling the RSI function
my_data = rsi(my_data, lookback_rsi, 3, 4)# Calling the ATR function to be used in the SuperTrend
my_data = atr(my_data, lookback_supertrend, 1, 2, 3, 5, genre = 'Smoothed')# Calling the SuperTrend Indicator
my_data = supertrend(my_data, multiplier, 5, 3, 1, 2, 6)The strategy is based on the flip from the SuperTrend with the condition that the RSI is above its 50% neutrality level. This reinforces the bullish bias and vice versa for the bearish bias.
A buy (Long) signal is generated whenever the SuperTrend Indicator flips below the market price while the RSI is above 50%.
A sell (Short) signal is generated whenever the SuperTrend Indicator flips above the market price while the RSI is below 50%.
def signal(Data, close, rsi_column, supertrend_column, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, rsi_column] > 50 and Data[i, close] > Data[i, supertrend_column] and Data[i - 1, close] < Data[i - 1, supertrend_column]:
Data[i, buy] = 1
elif Data[i, rsi_column] < 50 and Data[i, close] < Data[i, supertrend_column] and Data[i - 1, close] > Data[i - 1, supertrend_column]:
Data[i, sell] = -1
return DataThe strategy in its default form is unlikely to provide valuable signals and must be tweaked so that it captures better signals. Perhaps further research might show better signals?
If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.