Trading strategies come in all shapes and forms and creativity is something we need to always be following with regards to opportunities. Many technical strategies remain untouched but have a lot of potential. It is our duty to find them, mine them until they are exhausted. This article presents a simple strategy based on the Parabolic Stop-And-Reverse indicator and the RSI.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below Amazon link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Parabolic SAR
The Parabolic Stop-And-Reverse is an interesting trend-following indicator created by Wilder Willes who is also the creator of the famous RSI. This indicator is mostly used as a trailing stop that tracks the trend as it develops but there is no harm in testing it as a trading strategy. It is worth noting that it performs relatively well in steady trends but just as any other indicator, it has its weakness, in this case, ranging markets.
I will refer to a python library called talib from where the user could import the sar function that uses a data frame and calculates the values. Having modified that function, you can refer to the one below (I do not take credit for it as I merely just changed some lines as opposed to the other functions which have been coded by me):
def sar(s, af = 0.02, amax = 0.2):
high, low = s.high, s.low # Starting values
sig0, xpt0, af0 = True, high[0], af
sar = [low[0] - (high - low).std()] for i in range(1, len(s)):
sig1, xpt1, af1 = sig0, xpt0, af0 lmin = min(low[i - 1], low[i])
lmax = max(high[i - 1], high[i]) if sig1:
sig0 = low[i] > sar[-1]
xpt0 = max(lmax, xpt1)
else:
sig0 = high[i] >= sar[-1]
xpt0 = min(lmin, xpt1) if sig0 == sig1:
sari = sar[-1] + (xpt1 - sar[-1])*af1
af0 = min(amax, af1 + af) if sig0:
af0 = af0 if xpt0 > xpt1 else af1
sari = min(sari, lmin)
else:
af0 = af0 if xpt0 < xpt1 else af1
sari = max(sari, lmax)
else:
af0 = af
sari = xpt0 sar.append(sari) return sarThe basic understanding is that when the Parabolic SAR (the black dots around the market price) is under the current price, then the outlook is bullish and when it is above the current price, then the outlook is bearish.
To add the Parabolic SAR to your OHLC array, use the following steps:
# If you have an array
my_data = pd.DataFrame(my_data)# Renaming the columns to fit the function
my_data.columns = ['open','high','low','close']# Calculating the Parabolic SAR
Parabolic = sar(my_data, 0.01, 0.2)# Converting the Parabolic values back to an array
Parabolic = np.array(Parabolic)# Reshaping
Parabolic = np.reshape(Parabolic, (-1, 1))# Concatenating with the OHLC Data
my_data = np.concatenate((my_data, Parabolic), axis = 1)The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret.
Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data filedef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback) return DataIf you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Creating the Parabolic RSI Strategy
The aim is to apply the Parabolic SAR function on the values of the RSI so that it predicts momentum and indirectly gives some insights on the market’s state. I am of course in no way assuming that this is predictive method as it is too complex and lagging but it may offer good timing opportunities. However, the Parabolic SAR uses the highs and lows in its formula. How to address this problem? Simple, we will calculate the RSI values on the totality of the OHLC data (For convenience as the open price RSI is not really needed).
# Indicator Parameters
lookback_rsi = 5# Calling the RSI function on the open price
my_data = rsi(my_data, lookback_rsi, 0, 4)# Calling the RSI function on the high price
my_data = rsi(my_data, lookback_rsi, 1, 5)# Calling the RSI function on the low price
my_data = rsi(my_data, lookback_rsi, 2, 6)# Calling the RSI function on the close price
my_data = rsi(my_data, lookback_rsi, 3, 7)Now, the Parabolic SAR function will take into account the RSI values instead of the actual OHLC price data. This way, we will have a Parabolic SAR that follows the 5-period RSI readings.
# If you have an array
my_data = pd.DataFrame(my_data)# Renaming the columns to fit the function
my_data.columns = ['open-original','high-original','low-original','close-original', 'open','high','low','close']# Calculating the Parabolic SAR
Parabolic = sar(my_data, 0.9, 0.2)# Converting the Parabolic values back to an array
Parabolic = np.array(Parabolic)# Reshaping
Parabolic = np.reshape(Parabolic, (-1, 1))# Concatenating with the OHLC Data
my_data = np.concatenate((my_data, Parabolic), axis = 1)Note that we tweaked a little bit the Parabolic SAR default parameters by putting (0.9, 0.2) for better reactivity.
It is clear from the above chart that we have a Parabolic SAR following the RSI’s values and confirming the bias.
def indicator_plot_double(Data, opening, high, low, close, second_panel, window = 250): fig, ax = plt.subplots(2, figsize = (10, 5)) Chosen = Data[-window:, ]
for i in range(len(Chosen)):
ax[0].vlines(x = i, ymin = Chosen[i, low], ymax = Chosen[i, high], color = 'black', linewidth = 1)
if Chosen[i, close] > Chosen[i, opening]:
color_chosen = 'green'
ax[0].vlines(x = i, ymin = Chosen[i, opening], ymax = Chosen[i, close], color = color_chosen, linewidth = 2) if Chosen[i, close] < Chosen[i, opening]:
color_chosen = 'red'
ax[0].vlines(x = i, ymin = Chosen[i, close], ymax = Chosen[i, opening], color = color_chosen, linewidth = 2)
if Chosen[i, close] == Chosen[i, opening]:
color_chosen = 'black'
ax[0].vlines(x = i, ymin = Chosen[i, close], ymax = Chosen[i, opening], color = color_chosen, linewidth = 2)
ax[0].grid()
ax[1].plot(Data[-window:, second_panel], color = 'royalblue', linewidth = 1)
ax[1].grid()indicator_plot_double(my_data, 0, 1, 2, 3, 7, window = 250)
plt.plot(my_data[-250:, 8], linestyle = 'dashed', color = 'purple', linewidth = 1)
plt.axhline(y = 25, color = 'black', linestyle = 'dashed', linewidth = 1)
plt.axhline(y = 75, color = 'black', linestyle = 'dashed', linewidth = 1)The trading strategy is simple, we will initiate contrarian positions based on the relationship between the RSI and its Parabolic SAR as well as the distance between the RSI and the extreme levels. The trading rules will be as follow:
A Buy (Long) signal is generated whenever the current 5-period RSI is greater than the current Parabolic SAR while the previous one is below it. Similarly, the current RSI must be below 35%.
A Sell (Short) signal is generated whenever the current 5-period RSI is below the current Parabolic SAR while the previous one is above it. Similarly, the current RSI must be above 65%.
def signal(Data, rsi_col, psar_col, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, rsi_col] > Data[i, psar_col] and Data[i - 1, rsi_col] < Data[i - 1, psar_col] and \
Data[i, rsi_col] < 35:
Data[i, buy] = 1 if Data[i, rsi_col] < Data[i, psar_col] and Data[i - 1, rsi_col] > Data[i - 1, psar_col] and \
Data[i, rsi_col] > 65:
Data[i, sell] = -1
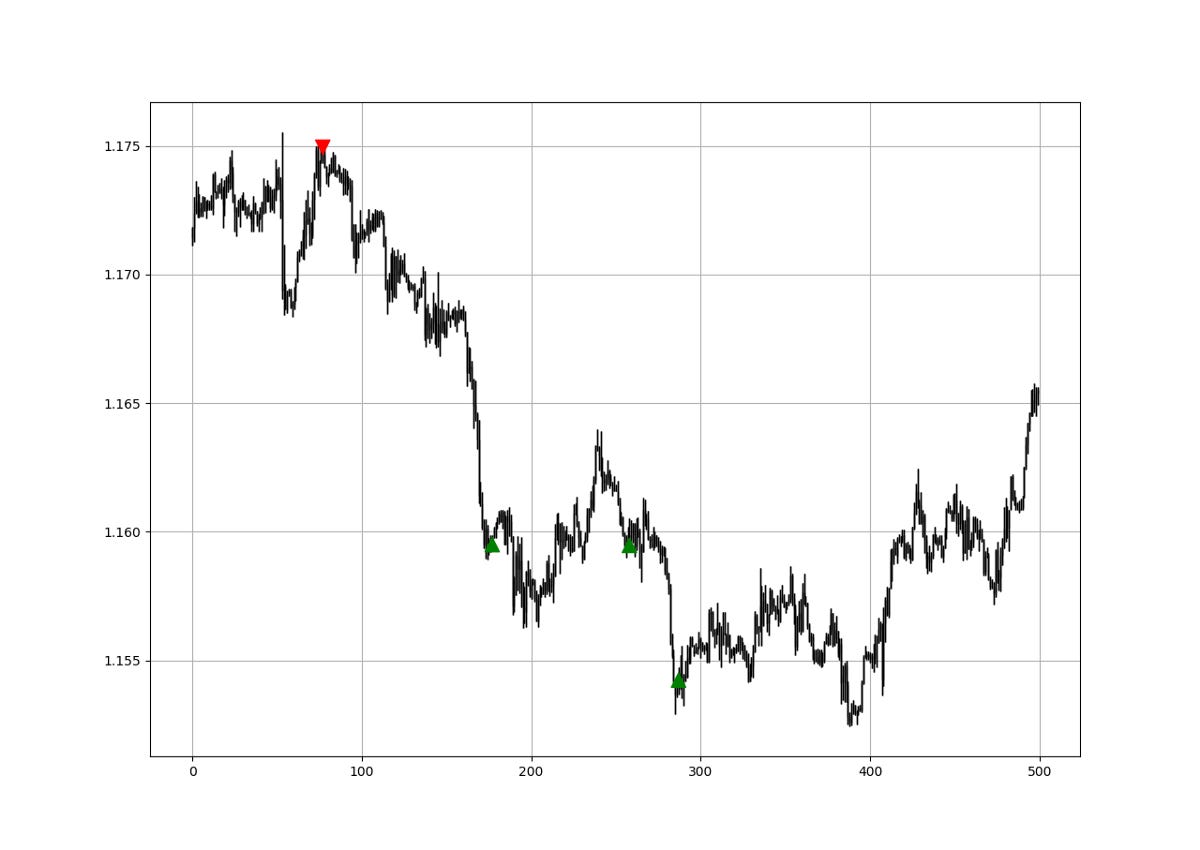
return DataThe below chart shows the signals generated following the strategy. The green arrows signify buy signals while the red arrows signify a sell short opportunity.
Every strategy must be optimized and tweaked so it reflects more the nature of the underlying market. Extensive back-testing must also take place in order to find the right fit. This is just an idea of a technical strategy.
The strategy can be a good addition to the discretionary framework in case we need an extra signal to fire off that trade. As every contrarian strategy out there, its weakness is a trending market.
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.