The great Bollinger Bands are one of the first things we must learn when analyzing time series. This is because of their sound statistical reasoning, their wide adoption across market participants, and their success when deployed in trading strategies. We can also see other variations that resemble the bands in an attempt to enhance it. This article will discuss the Fractal Adaptive Volatility Bands, a type of Bands indicator based on a special type of moving averages.
I have just released a new book after the success of my previous one “The Book of Trading Strategies”. It features advanced trend-following indicators and strategies with a GitHub page dedicated to the continuously updated code. Also, this book features the original colors after having optimized for printing costs. If you feel that this interests you, feel free to visit the below Amazon link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Fractal Adaptive Moving Average — FRAMA
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data filedef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return DataAs the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
The below states that the moving average function will be called on the array named my_data for a lookback period of 200, on the column indexed at 3 (closing prices in an OHLC array). The moving average values will then be put in the column indexed at 4 which is the one we have added using the adder function.
my_data = ma(my_data, 200, 3, 4)The Fractal Adaptive Moving Average — FRAMA is a complex type of moving averages which uses the Fractal Dimension Index — FDI as one of its components. We will see how to code the FRAMA before we move on to create the Fractal Adaptive Volatility Bands — FAVB.
The FDI measures how irregular the time series is. When there is a strong trend going on, naturally, the market price is approaching a one-dimensional line and the Fractal Dimension Index approaches 1.0. When the market is choppy and moving sideways, the Fractal Dimension Index approaches 2.0.
def fractal_dimension(Data, lookback, high, low, close, where):
Data = adder(Data, 10)
for i in range(len(Data)):
try:
# Calculating N1
Data[i, where] = max(Data[i - (2 * lookback):i - lookback, high])
Data[i, where + 1] = min(Data[i - (2 * lookback):i - lookback, low])
Data[i, where + 2] = (Data[i, where] - Data[i, where + 1]) / lookback
# Calculating N2
Data[i, where + 3] = max(Data[i - lookback:i, high])
Data[i, where + 4] = min(Data[i - lookback:i, low])
Data[i, where + 5] = (Data[i, where + 3] - Data[i, where + 4]) / lookback
# Calculating N3
Data[i, where + 6] = max(Data[i, where], Data[i, where + 3])
Data[i, where + 7] = min(Data[i, where + 1], Data[i, where + 4])
Data[i, where + 8] = (Data[i, where + 6] - Data[i, where + 7]) / (2 * lookback)
# Calculating the Fractal Dimension Index
if Data[i, where + 2] > 0 and Data[i, where + 5] > 0 and Data[i, where + 8] > 0:
Data[i, where + 9] = (np.log(Data[i, where + 2] + Data[i, where + 5]) - np.log(Data[i, where + 8])) / np.log(2)
except ValueError:
pass
# Cleaning
Data = deleter(Data, where, 9)
Data = jump(Data, lookback * 2)
return DataDeveloped by John Ehlers, the FRAMA is a special type of moving averages that uses exponential smoothing based on the current FDI calculated on the price. It is also adaptive in that it is able to follow strong moves and at the same time takes into account corrections and consolidations. The first thing we need to calculate with the FRAMA is the alpha factor. The alpha factor deals with the fractal smoothing part of the formula:
The above formula means that the alpha factor at any point in time equals the exponential function raised to the power of -4.6 multiplied by the current Fractal Dimension Index reading minus 1. Let us assume that we have defined the code of the FDI in the previous section and that we have an OHLC data array. To calculate a new column populated by the alpha factor, we follow this code:
# Indicator Parameters
lookback = 20# Calculating a 20-period Fractal Dimension Index
my_data = fractal_dimension(my_data, lookback, 1, 2, 3, 4)# Adding a Few Columns
my_data = adder(my_data, 1)# Calculating the alpha factor
for i in range(len(my_data)):
my_data[i, 5] = np.exp(-4.6 * (my_data[i, 4] - 1))The FRAMA is calculated following this below function.
# Calculating the First Value of FRAMA
my_data[1, 6] = (my_data[1, 5] * my_data[1, 3]) + ((1 - my_data[1, 5]) * my_data[0, 3])
# Calculating the Rest of FRAMA
for i in range(2, len(Data)):
try:
my_data[i, 6] = (my_data[i, 5] * my_data[i, 3]) + ((1 - my_data[i, 5]) * my_data[i - 1, 6])except IndexError:
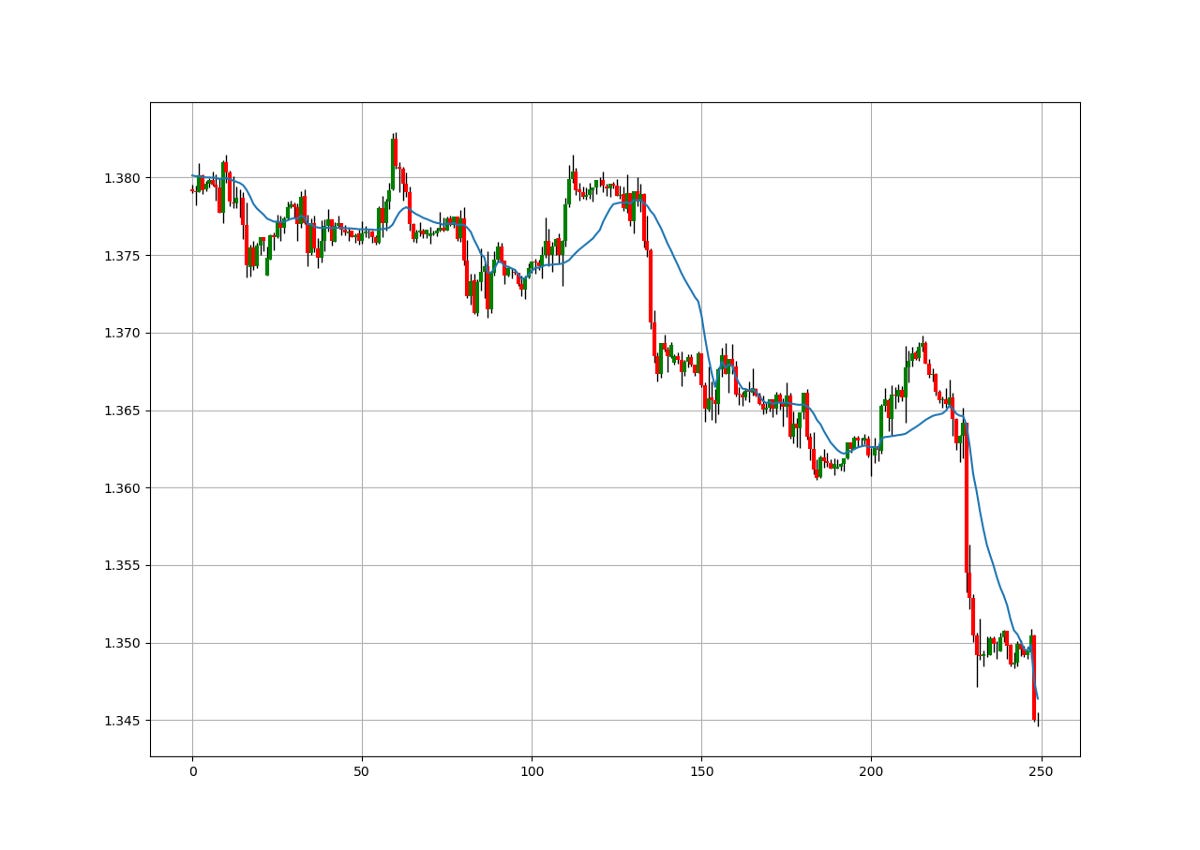
passThe above chart shows the EURUSD hourly values with the 20-period FRAMA. We can notice how it adapts to the dynamic market environment. Trading strategies based on this overlay indicator are the same as any other moving average.
The Fractal Adaptive Volatility Bands — FAVB
We are familiar with the Bollinger Bands where we use them to initiate contrarian positions whenever the market reaches the upper band or the lower band as we expect that statistically, the market is overbought or oversold, hence by using standard deviation we are able to have a view on the likely reaction of the market off current levels. The FAVB simply uses the same formula but deals with the FRAMA instead of the simple moving average.
lookback = 20
constant = 3# Calculating the FDI
my_data = fractal_dimension(my_data, lookback, 1, 2, 3, 4)# Adding a Few Columns
my_data = adder(my_data, 2)# Calculating the alpha factor
for i in range(len(my_data)):
my_data[i, 5] = np.exp(-4.6 * (my_data[i, 4] - 1))# Calculating the First Value of FRAMA
my_data[1, 6] = (my_data[1, 5] * my_data[1, 3]) + ((1 - my_data[1, 5]) * my_data[0, 3])# Calculating the Rest of FRAMA
for i in range(2, len(my_data)):
try:
my_data[i, 6] = (my_data[i, 5] * my_data[i, 3]) + ((1 - my_data[i, 5]) * my_data[i - 1, 6])
except IndexError:
pass # Cleaning
my_data = deleter(my_data, 5, 1)# Function of the standard deviation
def volatility(Data, lookback, what, where):
# Adding an extra column
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, what].std())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Data# Calculating the standard deviation
my_data = (volatility(my_data, lookback, 3, 6))# Multiplying by the constant
my_data[:, 6] = constant * my_data[:, 6]
my_data = adder(my_data, 10)# Upper FAVB
my_data[:, 7] = my_data[:, 5] + my_data[:, 6] # Lower FAVB
my_data[:, 8] = my_data[:, 5] - my_data[:, 6]A long (Buy) signal is generated when the low touches the lower band of the FAVB(20, 3)
A short (Sell) signal is generated when the high touches the upper band of the FAVB(20, 3)
def signal(Data, high, low, upper_band, lower_band, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, low] < Data[i, lower_band] and Data[i - 1, low] > Data[i - 1, lower_band]:
Data[i, buy] = 1
elif Data[i, high] > Data[i, upper_band] and Data[i - 1, high] < Data[i - 1, upper_band]:
Data[i, sell] = -1
return DataThe above chart shows the signals generated whenever the market approaches the bands. Interestingly, unlike the regular Bollinger bands, the FAVB is adjusted according to the fractal dimension of the market and is therefore as reactive as it is defensive. In some instances, the Bollinger bands will just follow the market and will show many signals, but the FAVB seems to have less false signals.
As usual, the volatility bands technique works well in ranging markets such as the USDCAD in the above chart and window.
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.