The Flat RSI Trading Technique — Researching Strategies in Python.
Creating a Strategy Based on the Flattening of the RSI.
The Relative Strength Index offers many possibilities of developing strategies around it. One such proposed strategy by Erich Florek is the flattening of the RSI². This technique might give some insights as to whether the current market is stalling or not.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def adder(Data, times):
for i in range(1, times + 1):
new = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new, axis = 1) return Datadef deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1) return Data
def jump(Data, jump):
Data = Data[jump:, ]
return Datadef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback) return DataThe RSI²
The RSI² is a very simple idea. The hypothesis is that the RSI is a stationary indicator and is more easily forecasted than the actual price chart. Hence, we apply an RSI to the RSI so that we use the second RSI (Which we call RSI²) to forecast the direction of the original RSI. Why do we do this? Because historically, the correlation between the market return and its own RSI (Change in value) is very high.
The limitations of this strategy is that we are using a transformation of a price-transformation indicator to predict semi-random data. This gives a huge weight to lift. Therefore, we will be running our strategy based on the intuition above with certain conditions that make it less prone to lag.
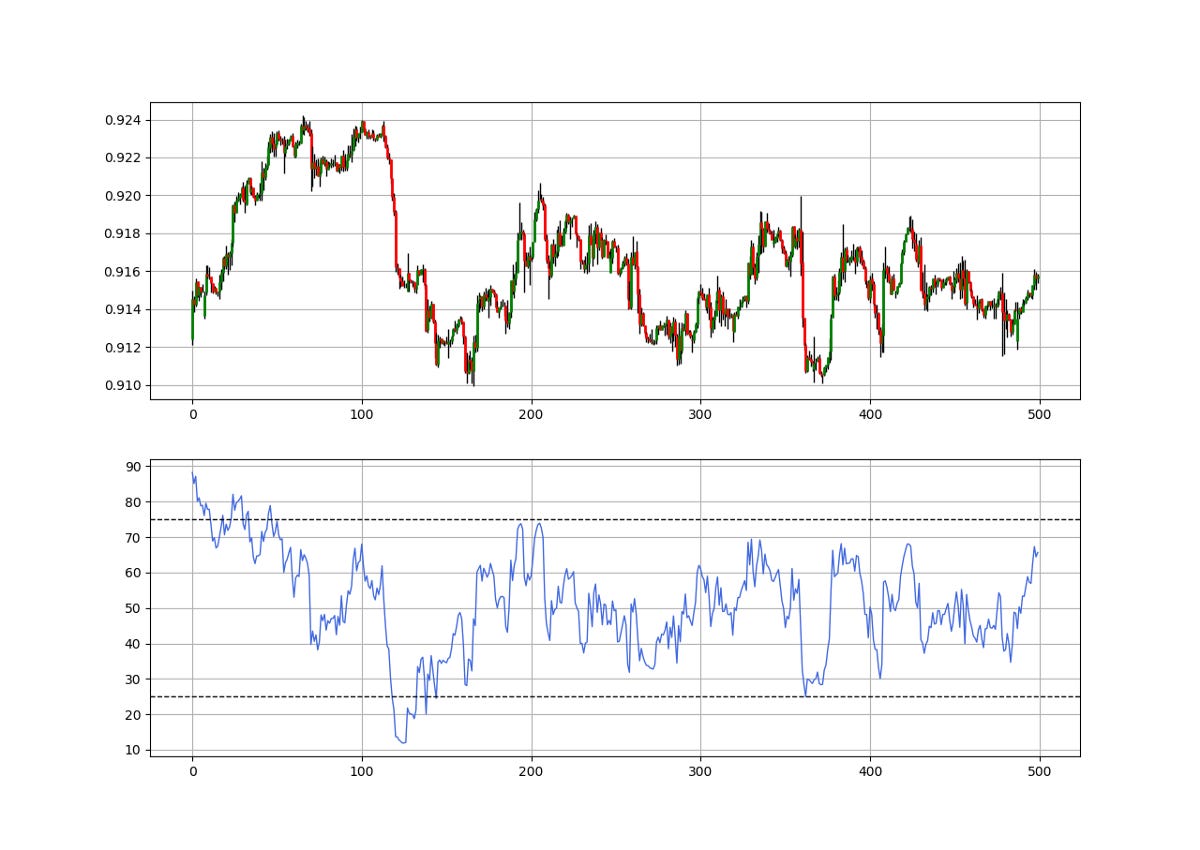
The Relative Strength Index is known for the extremes strategy (Oversold and Overbought levels) where we initiate contrarian positions when the RSI is close to the extremes in an attempt to fade the current trend. In this article, we will use a different strategy based on the flattening of the RSI² (in orange) when it is below a certain threshold.

The Flattening Strategy
The short-term RSI² will be the main protagonist of the strategy as we will use its flattening formations as signals. The trading conditions are therefore:
A buy (Long) signal is generated whenever the current 3-period RSI² is equal to the previous one while the two readings are below 40.
A sell (Short) signal is generated whenever the current 3-period RSI² is equal to the previous one while the two readings are above 60.
# Indicator Parameters
lookback = 3def signal(Data, indicator_column_second, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, indicator_column_second] == Data[i - 1, indicator_column_second] and Data[i, indicator_column_second] < 40:
Data[i, buy] = 1 elif Data[i, indicator_column_second] == Data[i - 1, indicator_column_second] and Data[i, indicator_column_second] > 60:
Data[i, sell] = -1
return Datamy_data = adder(my_data, 10)my_data = rsi(my_data, lookback, 3, 4)
my_data = rsi(my_data, lookback, 4, 5)my_data = signal(my_data, 5, 6, 7)If you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.