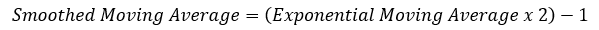The Choppiness Index - Detecting Trends & Sideways
Creating and Coding the Choppiness Index for Trading
Knowing when we are trending and when we are ranging is primordial to select which strategy we will use. After all, using Trend-Following systems on ranging markets will unlikely provide any profits. Similarly, using mean-reverting strategies will unlikely make us any money. In this article, we will look at an indicator that can help to detect the current market state. Surely, all indicators are inherently laggards but they are the best we have when transforming prices.
It is finally out! My newest book with O’Reilly Media on candlestick pattern recognition is now available on Amazon! The book features a huge number of classic and modern candlestick patterns as it dwelves into the realm of technical analysis with different trading strategies. The book comes with its own GitHub and is dynamic in nature as it is continuously updated and questions are answered on the O’Reilly platform.
Mastering Financial Pattern Recognition
Amazon.com: Mastering Financial Pattern Recognition eBook : Kaabar, Sofien: Kindle Storewww.amazon.com
Market State
Markets alternate between trending, mean-reverting, and randomness. The first two present trading opportunities that could be exploited by the use of strategies. The third one is where we should avoid trading as its randomness or choppiness makes it unlikely to predict its direction or at least to predict a reaction from a certain area. Basically:
When higher highs or lower lows are consistently observed, we know that the market is trending.
When the market is generally contained within two levels and cannot break nor surpass either, we know that the market is ranging.
When the market is too volatile, making false breakouts, and not respecting support/resistance levels, we know that it is choppy, meaning that visually, we cannot know whether we are in a trend or a range.
A lot of indicators can be used to determine this such as the average directional index, moving averages, and the trend intensity index. We will start to explore another indicator called the choppiness index which as its name suggests, measures the degree of choppiness, i.e. the degree to where we should avoid trading.
Creating the Choppiness Index Step-By-Step
The first step in calculating the index is by having our OHLC data ready in the form of an array. Now, assuming we have an array containing historical OHLC data, the next step is to define the primal functions that will allow us to manipulate the rows and columns inside our arrays:
def adder(data, times):
for i in range(1, times + 1):
new = np.zeros((len(data), 1), dtype = float)
data = np.append(data, new, axis = 1)return datadef deleter(data, index, times):
for i in range(1, times + 1):
data = np.delete(data, index, axis = 1)return data
def jump(data, jump):
data = data[jump:, ]
return dataNow, the formula below can be divided into the following parts:
Calculate the n-period average true range on the price.
Sum the n-period average true range Calculations.
Subtract the highest high from the lowest low of the last n period.
Apply the formula below to get the choppiness index.
First, we need to understand the average true range before we start filling the function. To understand the average true range, we must first understand the concept of volatility. It is a key concept in finance, whoever masters it holds a tremendous edge in the markets. Unfortunately, we cannot always measure and predict it with accuracy. Even though the concept is more important in options trading, we need it pretty much everywhere else. Traders cannot trade without volatility nor manage their positions and risk. Quantitative analysts and risk managers require volatility to be able to do their work.
In technical analysis, an indicator called the average true range -ATR- can be used as a gauge for historical volatility. Although it is considered lagging, it gives some insights as to where volatility is now and where has it been last period (day, week, month, etc.).
But first, we should understand how the true range is calculated (the ATR is just the average of that calculation). Consider an OHLC data composed of timely arrange open, high, low, and close prices. For each time period (bar), the true range is simply the greatest of the three price differences:
High — Low
High — Previous close
Previous close — Low
Once we have got the maximum out of the above three, we simply take a smoothed average of n periods of the true ranges to get the Average True Range. Generally, since in periods of panic and price depreciation we see volatility go up, the ATR will most likely trend higher during these periods, similarly, in times of steady uptrends or downtrends, the ATR will tend to go lower. One should always remember that this indicator is very lagging and therefore has to be used with extreme caution.
Since it has been created by Wilder Wiles, also the creator of the Relative Strength Index, it uses Wilder’s own type of moving average, the smoothed kind. To simplify things, the smoothed moving average can be found through a simple transformation of the exponential moving average.
The above formula means that a 100 smoothed moving average is the same thing as (100 x 2) -1 = 199 exponential moving average. While we are on that, we can code the exponential moving average using this function:
def ma(Data, lookback, what, where):
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, what].mean())
except IndexError:
pass
return Datadef ema(Data, alpha, lookback, what, where):
# alpha is the smoothing factor
# window is the lookback period
# what is the column that needs to have its average calculated
# where is where to put the exponential moving average
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return DataBelow is the function code that calculates the ATR.
def atr(data, lookback, high, low, close, where):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = max(data[i, high] - data[i, low], abs(data[i, high] - data[i - 1, close]), abs(data[i, low] - data[i - 1, close]))
except ValueError:
pass
data[0, where] = 0
data = ema(data, 2, (lookback * 2) - 1, where, where + 1) data = deleter(data, where, 1)
data = jump(data, lookback)
return dataLet us try applying the code on OHLC data and see the plot of a 14-period Average True Range:
my_data = atr(my_data, 14, 1, 2, 3, 4)Now we are ready to continue with the choppiness index. Let us consider that we will calculate a 20-period Average True Range on our OHLC historical data:
# Adding a few columns
my_data = adder(my_data, 10)# Calculating a 20-period ATR
my_data = atr(my_data, 20, 1, 2, 3, 4)Now, the first step into the indicator is, to sum up, the values of the ATR together. This intuition can be coded in the following manner (Full function code provided below):
# Calculating the Sum of ATR's (atr_col is the index where the ATR is stored, in our example, it is 4)
for i in range(len(my_data)):my_data[i, where] = my_data[i - lookback + 1:i + 1, atr_col].sum()Now, we have to calculate the range from the highest to lowest using the max() and min() built-in functions. The code should resemble the following:
# Calculating the range
for i in range(len(my_data)):
try:
my_data[i, 5] = max(my_data[i - lookback + 1:i + 1, 1] - min(my_data[i - lookback + 1:i + 1, 2]))
except:
passNext, we calculate the ratio between the two measures we have just derived. The code can be as simple as:
# Calculating the Ratio
my_data[:, 6] = my_data[:, 4] / my_data[:, 5]And finally, we simply apply the function as presented above, using this code:
# Calculate the Choppiness Index
for i in range(len(Data)):
Data[i, 7] = 100 * np.log(Data[i, 6]) * (1 / np.log(20))def choppiness_index(Data, lookback, high, low, where):
# Calculating the Sum of ATR's
for i in range(len(Data)):
Data[i, where] = Data[i - lookback + 1:i + 1, 4].sum()
# Calculating the range
for i in range(len(Data)):
try:
Data[i, where + 1] = max(Data[i - lookback + 1:i + 1, 1] - min(Data[i - lookback + 1:i + 1, 2]))
except:
pass# Calculating the Ratio
Data[:, where + 2] = Data[:, where] / Data[:, where + 1]
# Calculate the Choppiness Index
for i in range(len(Data)):
Data[i, where + 3] = 100 * np.log(Data[i, where + 2]) * (1 / np.log(lookback))# Cleaning
Data = deleter(Data, 5, 3)
return DataThe choppiness index function can therefore be called using the following code:
my_data = choppiness_index(my_data, 20, 1, 2, 4)Using the Choppiness Index
The way to use the choppiness index is to place the barriers by default at 38.2% and 61.8%, then we interpret the readings as follow:
Readings above 61.8% indicate a choppy market that is bound to breakout. We should be ready for some directional.
Readings below 38.2% indicate a strong trending market that is bound to stabilize. Hence, it may not be the best idea to follow the trend at the moment.
If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.