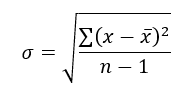The Catapult Indicator
Presenting the Volatility-Based Catapult Indicator in Python
Just like a catapult, this technical indicator is based on three systems which deal with Volatility (Acting as the fulcrum), Momentum (Acting as a payload propeller, and a Directional Filter (Acting as the support). The aim is to get a signal that predicts an acceleration of volatility based on previous patterns as well as the direction following this volatility. Therefore, we are aiming to answer an important question, when will the market move? and where? Surely, no answer is perfect, but this indicator has shown better results than other classical indicators.
Start your Free Trial now at O’Reilly and start reading the Early Release of my upcoming book “Mastering Financial Pattern Recognition” which covers everything you need to know about candlestick patterns and how to code them in Python! (Bonus points: You will discover new never-seen-before patterns). You will also find technical indicators, risk management, and even behavioral finance covered in the book!
Mastering Financial Pattern Recognition
Candlesticks have become a key component of platforms and charting programs for financial trading. With these charts…www.oreilly.com
The Base Part: Volatility
For the volatility part, the Catapult uses the 21-period Relative Volatility Index to predict the big moves.
There are many ways to measure volatility such as the Average True Range, the Mean Absolute Deviation, and the Standard Deviation. We will use Standard Deviation to create the Relative Volatility Index.
The most basic type of volatility is the Standard Deviation. It is one of the pillars of descriptive statistics and an important element in some technical indicators such as the famous Bollinger Bands. But first let us define what Variance is before we find the Standard Deviation.
Variance is the squared deviations from the mean (a dispersion measure), we take the square deviations so as to force the distance from the mean to be non-negative, finally we take the square root to make the measure have the same units as the mean, in a way we are comparing apples to apples (mean to standard deviation standard deviation). Variance is calculated through this formula:
Following what we have said, standard deviation is therefore:
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data filedef volatility(Data, lookback, what, where):
for i in range(len(Data)):try:Data[i, where] = (Data[i - lookback + 1:i + 1, what].std())except IndexError:pass
return DataThe exciting job now is to turn the historical volatility otherwise known as the historical Standard Deviation into a measure that allows us to predict whether there will be an outburst of volatility or not. This will simply be done by applying the formula of the Relative Strength Index — RSI on the values of the standard deviation.
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
def ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)return Datadef relative_volatility_index(Data, lookback, close, where):# Calculating Volatility
Data = volatility(Data, lookback, close, where)
# Calculating the RSI on Volatility
Data = rsi(Data, lookback, where, where + 1)
# Cleaning
Data = deleter(Data, where, 1)
return DataKnowledge must be accessible to everyone. This is why, from now on, a purchase of either one of my new books “Contrarian Trading Strategies in Python” or “Trend Following Strategies in Python” comes with free PDF copies of my first three books (Therefore, purchasing one of the new books gets you 4 books in total). The two new books listed above feature a lot of advanced indicators and strategies with a GitHub page. You can use the below link to purchase one of the two books (Please specify which one and make sure to include your e-mail in the note).
Pay Kaabar using PayPal.Me
Go to paypal.me/sofienkaabar and type in the amount. Since it’s PayPal, it’s easy and secure. Don’t have a PayPal…www.paypal.com
The Arm Part: Momentum
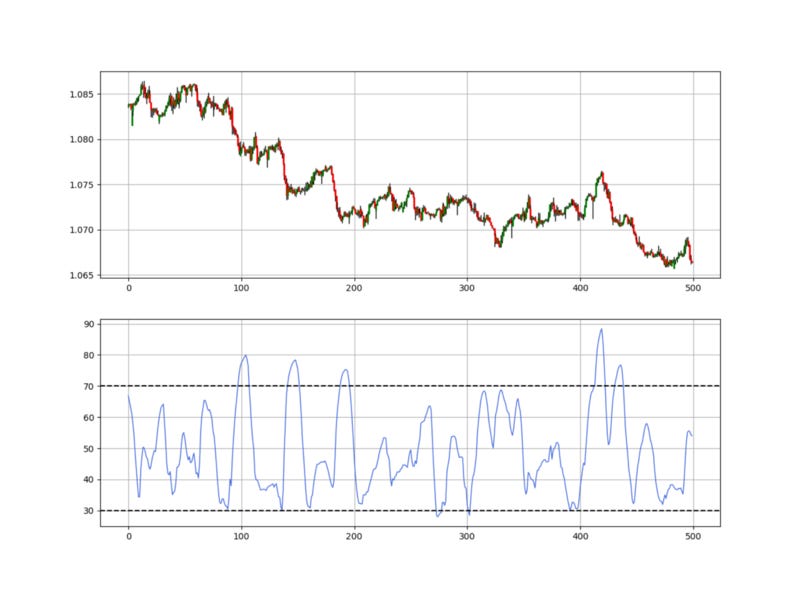
For the momentum part, the Catapult uses the 14-period Relative Strength Index to predict the likelihood direction of the move.
As a reminder, the RSI is bounded between 0 and 100 where we can identify two levels from where contrarian signals are generated:
The oversold level 30 is where the market is perceived to have gone down too much and a bullish reaction is to be expected.
The overbought level 70 is where the market is perceived to have gone up too much and a bearish reaction is to be expected.
Another interesting way to use the RSI is by comparing the current reading to the 50 level. If the RSI is above 50, then a likely bullish momentum is in place and if it is below 50, then a likely bearish momentum is in place.
Make sure to focus on the concepts and not the code. The most important thing is to comprehend the techniques and strategies. The code is a matter of execution but the idea is something you cook in your head for a while.
The Frame Part: Directional Filter
For the directional filter part, the Catapult uses the 200-period simple moving average to keep us in the direction of the trend. This serves as a sanity check and to stack more odds with us.
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
As the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
We have seen in the above sections how to define the moving average function. Now, we are ready to create the Catapult indicator.
The Catapult Indicator
The indicator is based on a healthy mix of the above three indicators where:
The 21-period Relative Volatility Index will give the first trigger by stating that as of now, there will be above average volatility and therefore, possible a directional move.
The 14-period Relative Strength Index will give the likelihood direction of the move by saying that if the reading is above 50, then the move is likely bullish while if the reading is below 50, then the move is likely bearish.
The 200-period simple moving average will add conviction to the likelihood direction of the move. If the market is above the 200-period moving average then we understand that there is bullish pressure and quite likely a continuation to the upside. Similarly, if the market is below the 200-period moving average then we understand that there is bearish pressure and quite likely a continuation to the downside.
lookback_rvi = 21
lookback_rsi = 14
lookback_ma = 200my_data = ma(my_data, lookback_ma, 3, 4)
my_data = rsi(my_data, lookback_rsi, 3, 5)
my_data = relative_volatility_index(my_data, lookback_rvi, 3, 6)The Catapult is an overlay indicator with two handles. The first shows blue and green arrows which signify a buy signal and the second shows blue and red arrows which signify a sell signal.
The below chart shows a real life example on the most recent values on the hourly EURUSD.
def signal(Data, rvi_col, signal):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, rvi_col] < 30 and \
Data[i - 1, rvi_col] > 30 and \
Data[i - 2, rvi_col] > 30 and \
Data[i - 3, rvi_col] > 30 and \
Data[i - 4, rvi_col] > 30 and \
Data[i - 5, rvi_col] > 30:
Data[i, signal] = 1
return DataThe signals are quite easy and simple to understand. Surely, the indicator can be used alongside other strategies.
my_data = signal(my_data, 6, 7)If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.