The Candlestick-RSI — Innovative Pattern Recognition Trading Techniques.
Transforming the RSI Into a Candlestick Indicator Using Python.
Candlestick charting does not have to be limited to price data. What if it can be used on technical indicators so that start testing some new pattern recognition techniques? In this article, the RSI is looked at from the perspective of a simple candlestick chart where trading signals are derived. The basic idea is to start thinking about finding a robust strategy that uses the technique of applying candlesticks to technical indicators in order to find either hidden patterns or trend reversal confirmation signals.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. The RSI is notably used in many ways, among them:
The extremes strategy: Where we search for overbought an oversold levels to initiate contrarian trades. The idea is that an overbought market has a high reading on the RSI signifying too much bullish momentum and a possible correction or even a reversal may take place. Similarly, an oversold market has a low reading on the RSI signifying too much bearish momentum and a possible correction or even a reversal may take place.
The divergence strategy: When there is an established trend, the overall direction does not move linearly with regards to magnitude and force, meaning that when a market is rising, its momentum strength is not stable. At the beginning it is usually strong but by profit taking and lower convictions, the market starts to lose some strength, thus, continuing to rise but struggling to do so. This is where we see a bearish divergence on the RSI. A divergence signifies the trend’s exhaustion and may signal a correction or even a reversal. Visually, a bearish divergence is when we see the market making higher highs while the RSI is making lower highs. Similarly, a bullish divergence is when we see the market making lower lows while the RSI is making higher lows.
The fact that it is famous, contributes to the efficacy of the RSI. This is because the more traders and portfolio managers look at the indicator, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index through the following function, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)
return DataWe need to define the primal manipulation functions first in order to use the RSI’s function on OHLC data arrays.
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data
# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data
# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)
# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)
# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)
# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data fileCandlestick Charting
Candlestick charts are among the most famous ways to analyze the time series visually. They contain more information than a simple line chart and have more visual interpretability than bar charts. Many libraries in Python offer charting functions but being someone who suffers from malfunctioning import of libraries and functions alongside their fogginess, I have created my own simple function that charts candlesticks manually with no exogenous help needed.
OHLC data is an abbreviation for Open, High, Low, and Close price. They are the four main ingredients for a timestamp. It is always better to have these four values together so that our analysis reflects more the reality. Here is a table that summarizes the OHLC data of hypothetical security:
Our job now is to plot the data so that we can visually interpret what kind of trend is the price following. We will start with the basic line plot before we move on to candlestick plotting.
Note that you can download the data manually or using Python. In case you have an excel file that has OHLC only data starting from the first row and column, you can import it using the below code snippet:
import numpy as np
import pandas as pd
# Importing the Data
my_ohlc_data = pd.read_excel('my_ohlc_data.xlsx')
# Converting to Array
my_ohlc_data = np.array(my_ohlc_data)Plotting basic line plots is extremely easy in Python and requires only one line of code. We have to make sure that we have imported a library called matplotlib and then we will call a function that plots the data for us.
# Importing the necessary charting library
import matplotlib.pyplot as plt
# The syntax to plot a line chart
plt.plot(my_ohlc_data, color = 'black', label = 'EURUSD')
# The syntax to add the label created above
plt.legend()
# The syntax to add a grid
plt.grid()Now that we have seen how to create normal line charts, it is time to take it to the next level with candlestick charts. The way to do this with no complications is to think about vertical lines. Here is the intuition (followed by an application of the function below):
Select a lookback period. This is the number of values you want to appear on the chart.
Plot vertical lines for each row representing the highs and lows. For example, on OHLC data, we will use a matplotlib function called vlines which plots a vertical line on the chart using a minimum (low) value and a maximum (high value).
Make a color condition which states that if the closing price is greater than the opening price, then execute the selected block of code (which naturally contains the color green). Do this with the color red (bearish candle) and the color black (Doji candle).
Plot vertical lines using the conditions with the min and max values representing closing prices and opening prices. Make sure to make the line’s width extra big so that the body of the candle appears sufficiently enough that the chart is deemed a candlestick chart.
def ohlc_plot(Data, window, name):
Chosen = Data[-window:, ]
for i in range(len(Chosen)):
plt.vlines(x = i, ymin = Chosen[i, 2], ymax = Chosen[i, 1], color = 'black', linewidth = 1)
if Chosen[i, 3] > Chosen[i, 0]:
color_chosen = 'green'
plt.vlines(x = i, ymin = Chosen[i, 0], ymax = Chosen[i, 3], color = color_chosen, linewidth = 4)
if Chosen[i, 3] < Chosen[i, 0]:
color_chosen = 'red'
plt.vlines(x = i, ymin = Chosen[i, 3], ymax = Chosen[i, 0], color = color_chosen, linewidth = 4)
if Chosen[i, 3] == Chosen[i, 0]:
color_chosen = 'black'
plt.vlines(x = i, ymin = Chosen[i, 3], ymax = Chosen[i, 0], color = color_chosen, linewidth = 4)
plt.grid()
plt.title(name)
# Using the function
ohlc_plot(my_ohlc_data, 50, '')The Candlestick-RSI
The Candlestick RSI will be a regular 13-period RSI applied to the open prices and the closing prices, thus forming a simplistic type of candles where we can start seeing the psychology of the move. We can also add the high and low calculations so that we add them later into the signal. Therefore, the first step into creating the indicator is the following syntax:
lookback = 13
# Calculating a 13-period RSI on opening prices
my_data = rsi(my_data, lookback, 0, 5, genre = 'Smoothed')
# Calculating a 13-period RSI on high prices
my_data = rsi(my_data, lookback, 1, 6, genre = 'Smoothed')
# Calculating a 13-period RSI on low prices
my_data = rsi(my_data, lookback, 2, 7, genre = 'Smoothed')
# Calculating a 13-period RSI on closing prices
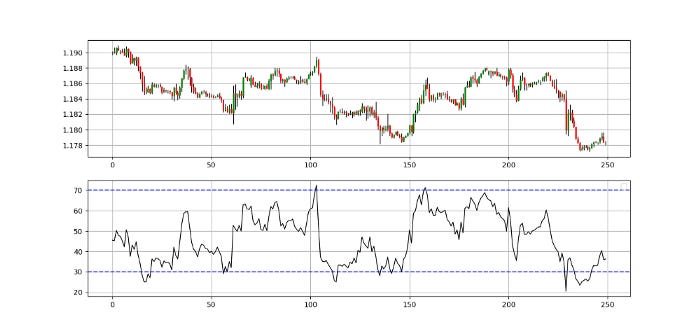
my_data = rsi(my_data, lookback, 3, 8, genre = 'Smoothed')The below chart shows the candlestick RSI in the first panel with the EURUSD hourly values in the second panel.
The above chart is a bit unusual, as we are used to putting the market price in the first panel. This time, we have switched and put the Candlestick-RSI above. We are now ready to derive the trading conditions based on a choice of candlestick patterns and the usual extremes strategy on the RSI.
The above chart shows an example on the USDCAD where barriers of 20 and 80 are more suited to the Candlestick RSI. Note that the word barriers refer to the oversold/overbought levels.
If you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Applying the Pattern Recognition Strategy
By fetching the conditions from candlestick pattern recognition and the RSI’s contrarian methods, we can develop the following trading rules:
Go long (Buy) whenever the current RSI (Based on closing prices) is greater than the current RSI (Based on opening prices) while simultaneously the current RSI (Based on low prices) is lower than the lower barrier of 20 (or 30 in the case of certain currency pairs).
Go short (Sell) whenever the current RSI (Based on closing prices) is lower than the current RSI (Based on opening prices) while simultaneously the current RSI (Based on high prices) is higher than the upper barrier of 80 (or 70 in the case of certain currency pairs).
def signal(Data):
Data = adder(Data, 20)
for i in range(len(Data)):
if Data[i, 8] > Data[i, 5] and Data[i, 7] < lower_barrier and Data[i - 1, 9] == 0:
Data[i, 9] = 1
elif Data[i, 8] < Data[i, 5] and Data[i, 6] > upper_barrier and Data[i - 1, 10] == 0:
Data[i, 10] = -1
return DataEvaluating the Signal Quality
Having had the signals, we now know when the algorithm would have placed its buy and sell orders, meaning, that we have an approximate replica of the past where can can control our decisions with no hindsight bias. We have to simulate how the strategy would have done given our conditions.
This means that we need to calculate the returns and analyze the performance metrics. Let us see a neutral metric that can give us somewhat a clue on the predictability of the indicator or the strategy. For this study, we will use the Signal Quality metric.
The signal quality is a metric that resembles a fixed holding period strategy. It is simply the reaction of the market after a specified time period following the signal. Generally, when trading, we tend to use a variable period where we open the positions and close out when we get a signal on the other direction or when we get stopped out (either positively or negatively). Sometimes, we close out at random time periods. Therefore, the signal quality is a very simple measure that assumes a fixed holding period and then checks the market level at that time point to compare it with the entry level. In other words, it measures market timing by checking the reaction of the market. For the performance evaluation to be unbiased, we will use three signal periods:
3 closing bars: This signal period relates to quick market timing strategies based on immediate reactions. In other words, we will be measuring the difference between the closing price 3 periods after the signal and the entry price at the trigger.
8 closing bars: This signal period relates to market timing strategies with some slight lag. In other words, we will be measuring the difference between the closing price 8 periods after the signal and the entry price at the trigger.
21 closing bars: This signal period relates to more important reactions that can even signal a change in the trend. In other words, we will be measuring the difference between the closing price 21 periods after the signal and the entry price at the trigger.
# Choosing an example of 3 periods
period = 3
def signal_quality(Data, closing, buy, sell, period, where):
Data = adder(Data, 1)
for i in range(len(Data)):
if Data[i, buy] == 1:
Data[i + period, where] = Data[i + period, closing] - Data[i, closing] if Data[i, sell] == -1:
Data[i + period, where] = Data[i, closing] - Data[i + period, closing]
return Data
# Using 3 Periods as a Window of signal Quality Check
my_data = signal_quality(my_data, 3, 6, 7, period, 8)
positives = my_data[my_data[:, 8] > 0]
negatives = my_data[my_data[:, 8] < 0]
# Calculating Signal Quality
signal_quality = len(positives) / (len(negatives) + len(positives))
print('Signal Quality = ', round(signal_quality * 100, 2), '%')
# Output for 3 periods USDCAD Hourly: 53.42%
# Output for 8 periods USDCAD Hourly: 50.75%
# Output for 21 periods USDCAD Hourly: 51.09%Unlimited tweaking and patterns can be tested on this interesting and promising field. We will do that in the coming articles in further details.
Conclusion & Important Disclaimer
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.