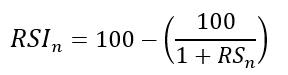Mixing the RSI With the Fisher Transform in a Trading Strategy.
Can the RSI and the Fisher Transform Provide Good Signals?
The relative strength index (RSI) is a great contrarian indicator. Similarly, the Fisher transform also can hint at possible market inflections. What if we try to combine the two together to give us a timely signal of when a reaction should occur. This means that we will use the RSI and the Fisher transform as a fused indicator that gives out contrarian signals based on its values. The first two parts will introduce the RSI and the Fisher transform and the third part will present the strategy.
The Relative Strength Index
First introduced by J. Welles Wilder Jr., the RSI is one of the most popular and versatile technical indicators. Mainly used as a contrarian indicator where extreme values signal a reaction that can be exploited. Typically, we use the following steps to calculate the default RSI:
Calculate the change in the closing prices from the previous ones.
Separate the positive net changes from the negative net changes.
Calculate a smoothed moving average on the positive net changes and on the absolute values of the negative net changes.
Divide the smoothed positive changes by the smoothed negative changes. We will refer to this calculation as the Relative Strength — RS.
Apply the normalization formula shown below for every time step to get the RSI.
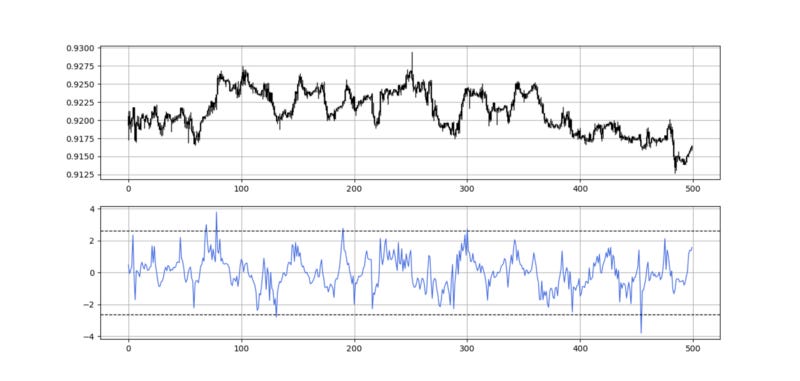
The above chart shows the hourly values of the GBPUSD in black with the 13-period RSI. We can generally note that the RSI tends to bounce close to 25 while it tends to pause around 75. To code the RSI in Python, we need an OHLC array composed of four columns that cover open, high, low, and close prices.
def adder(data, times):
for i in range(1, times + 1):
new = np.zeros((len(data), 1), dtype = float)
data = np.append(data, new, axis = 1) return datadef deleter(data, index, times):
for i in range(1, times + 1):
data = np.delete(data, index, axis = 1) return data
def jump(data, jump):
data = data[jump:, ]
return datadef ma(data, lookback, close, where):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = (data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
data = jump(data, lookback)
return datadef ema(data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
data = ma(data, lookback, what, where) data[lookback + 1, where] = (data[lookback + 1, what] * alpha) + (data[lookback, where] * beta) for i in range(lookback + 2, len(data)):
try:
data[i, where] = (data[i, what] * alpha) + (data[i - 1, where] * beta)
except IndexError:
pass
return datadef rsi(data, lookback, close, where):
data = adder(data, 5)
for i in range(len(data)):
data[i, where] = data[i, close] - data[i - 1, close]
for i in range(len(data)):
if data[i, where] > 0:
data[i, where + 1] = data[i, where]
elif data[i, where] < 0:
data[i, where + 2] = abs(data[i, where])
lookback = (lookback * 2) - 1 # From exponential to smoothed
data = ema(data, 2, lookback, where + 1, where + 3)
data = ema(data, 2, lookback, where + 2, where + 4) data[:, where + 5] = data[:, where + 3] / data[:, where + 4]
data[:, where + 6] = (100 - (100 / (1 + data[:, where + 5]))) data = deleter(data, where, 6)
data = jump(data, lookback) return dataThe Fisher Transform
One of the pillars of descriptive statistics is the normal distribution curve. It describes how random variables are distributed and centered around a central value. It often resembles a bell. Some data in the world are said to be normally distributed. This means that their distribution is symmetrical with 50% of the data lying to the left of the mean and 50% of the data lying to the right of the mean. Its mean, median, and mode are also equal as seen in the below curve.
The above curve shows the number of values within a number of standard deviations. For example, the area shaded in red represents around 1.33x of standard deviations away from the mean of zero. We know that if data is normally distributed then:
About 68% of the data falls within 1 standard deviation of the mean.
About 95% of the data falls within 2 standard deviations of the mean.
About 99% of the data falls within 3 standard deviations of the mean.
Presumably, this can be used to approximate the way to use financial returns data, but studies show that financial data is not normally distributed. For the moment, we can assume it is so that we can use such indicators. The flaw of the method does not hinder much its usefulness.
Let us now see how to create the modified Fisher transformation which is basically like the original one but with some minor changes to enhance the results and make them easier to obtain.
Created John F. Ehlers, the indicator seeks to transform the price into a normal Gaussian (normal) distribution. The steps to create the modified Fisher transformation are somewhat similar to the original Fisher Transformation. Here is how we do it:
Select a lookback period and calculate a normalized version of the OHLC data using the original Stochastic formula as seen in the formula below:
Trap the values from the first step between -1 and +1 using the following normalization formula:
Create a condition that eliminates the -1.00’s and +1.00’s and transforms them into -0.999’s and +0.999’s so that we do not get infinite values. This also serves to make the indicator bounded between two levels we will see later.
Apply the following formula to the results from the last step:
Now that we have the Modified Fisher Transformation Indicator, we can proceed by coding it in Python before starting the back-tests. The below plot shows a 5-period Modified Fisher Transformation with subjective boundaries at -2.00 and +2.00.
def stochastic_oscillator(data,
lookback,
high,
low,
close,
where,
slowing = False,
smoothing = False,
slowing_period = 1,
smoothing_period = 1):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = (data[i, close] - min(data[i - lookback + 1:i + 1, low])) / (max(data[i - lookback + 1:i + 1, high]) - min(data[i - lookback + 1:i + 1, low]))
except ValueError:
pass
data[:, where] = data[:, where] * 100
if slowing == True and smoothing == False:
data = ma(data, slowing_period, where, where + 1)
if smoothing == True and slowing == False:
data = ma(data, smoothing_period, where, where + 1)
if smoothing == True and slowing == True:
data = ma(data, slowing_period, where, where + 1)
data = ma(data, smoothing_period, where, where + 2)
data = jump(data, lookback) return datadef fisher_transform(data, lookback, high, low, close, where):
data = adder(data, 1)
data = stochastic_oscillator(data, lookback, high, low, close, where)
data[:, where] = data[:, where] / 100
data[:, where] = (2 * data[:, where]) - 1
for i in range(len(data)):
if data[i, where] == 1:
data[i, where] = 0.999
if data[i, where] == -1:
data[i, where] = -0.999
for i in range(len(data)):
data[i, where + 1] = 0.5 * (np.log((1 + data[i, where]) / (1 - data[i, where])))
data = deleter(data, where, 1)
return dataNaturally with the correction I have added, the maximum values will be 3.80 and the minimum values will be -3.80. Therefore, we can say that the indicator is now bounded even though the original version was not shown to be bounded.
Creating the Strategy
The indicator or index we will create is formed by the two indicators above as already mentioned. We will below see how to create it.
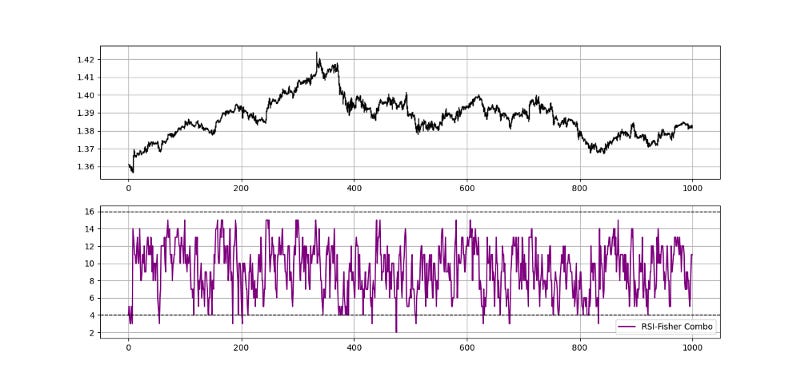
Combining indicators and techniques is the first step towards a robust trading system as getting a confluence of signals around a time period reinforces the conviction. There are many ways to create such structured strategies namely, scorecards, indices, and simultaneous conditions. The strategy we will be discussing will revolve around a form of an index where the values from both indicators are transformed to be between 0 and 10. Hence, the RSI-Fisher will be an indicator that ranges between 0 and 20 composed of the RSI (on a scale of 0 to 10) and the modified Fisher transform (on a scale of 0 to 10).
The conditions we will be using for this strategy (as opposed to the above plots) are:
Long (Buy) whenever the 3-period RSI-Fisher combo reaches 4.
Short (Sell) whenever the 3-period RSI-Fisher combo reaches 14.
# Transformation process on the RSI
for i in range(len(my_data)):
if my_data[i, 4] > 0 and my_data[i, 4] <= 10:
my_data[i, 4] = 0 elif my_data[i, 4] > 10 and my_data[i, 4] <= 20:
my_data[i, 4] = 1 elif my_data[i, 4] > 20 and my_data[i, 4] <= 30:
my_data[i, 4] = 2 elif my_data[i, 4] > 30 and my_data[i, 4] <= 40:
my_data[i, 4] = 3 elif my_data[i, 4] > 40 and my_data[i, 4] <= 50:
my_data[i, 4] = 4 elif my_data[i, 4] > 50 and my_data[i, 4] <= 60:
my_data[i, 4] = 5 elif my_data[i, 4] > 60 and my_data[i, 4] <= 70:
my_data[i, 4] = 6 elif my_data[i, 4] > 70 and my_data[i, 4] <= 80:
my_data[i, 4] = 7 elif my_data[i, 4] > 80 and my_data[i, 4] <= 90:
my_data[i, 4] = 8 elif my_data[i, 4] > 90 and my_data[i, 4] <= 100:
my_data[i, 4] = 9 elif my_data[i, 4] == 100:
my_data[i, 4] = 10# Transformation process on the Modified Fisher Transform
for i in range(len(my_data)):
if my_data[i, 5] > -4 and my_data[i, 5] <= -3.5:
my_data[i, 5] = 0
elif my_data[i, 5] > -3.5 and my_data[i, 5] <= -3:
my_data[i, 5] = 1
elif my_data[i, 5] > -3 and my_data[i, 5] <= -2:
my_data[i, 5] = 2
elif my_data[i, 5] > -2 and my_data[i, 5] <= -1:
my_data[i, 5] = 3
elif my_data[i, 5] > -1 and my_data[i, 5] <= 0:
my_data[i, 5] = 4
elif my_data[i, 5] > 0 and my_data[i, 5] <= 1:
my_data[i, 5] = 5
elif my_data[i, 5] > 1 and my_data[i, 5] <= 2:
my_data[i, 5] = 6
elif my_data[i, 5] > 2 and my_data[i, 5] <= 3:
my_data[i, 5] = 7
elif my_data[i, 5] > 3 and my_data[i, 5] <= 3.5:
my_data[i, 5] = 8
elif my_data[i, 5] > 3.5 and my_data[i, 5] <= 4:
my_data[i, 5] = 9
elif my_data[i, 5] > 4:
my_data[i, 5] = 10Now, we are ready to write the signal function as mentioned above:
def signal(Data, what, buy, sell):
for i in range(len(Data)):
if Data[i, what] < lower_barrier and Data[i - 1, what] > lower_barrier and Data[i - 2, what] > lower_barrier :
Data[i, buy] = 1
if Data[i, what] > upper_barrier and Data[i - 1, what] < upper_barrier and Data[i - 2, what] < upper_barrier :
Data[i, sell] = -1Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.
One Last Word
I have recently started an NFT collection that aims to support different humanitarian and medical causes. The Society of Light is a set of limited collectibles which will help make the world slightly better as each sale will see a percentage of it sent directly to the charity attributed to the avatar. As I always say, nothing better than a bullet list to outline the benefits of buying these NFT’s:
High-potential gain: By concentrating the remaining sales proceedings on marketing and promoting The Society of Light, I am aiming to maximize their value as much as possible in the secondary market. Remember that trading in the secondary market also means that a portion of royalties will be donated to the same charity.
Art collection and portfolio diversification: Having a collection of avatars that symbolize good deeds is truly satisfying. Investing does not need to only have selfish needs even though there is nothing wrong with investing to make money. But what about investing to make money, help others, and collect art?
Donating to your preferred cause(s): This is a flexible way of allocating different funds to your charities.
A free copy of my book in PDF: Any buyer of any NFT will receive a free copy of my latest book shown in the link of the article.