Double Top / Double Bottom RSI Trading Strategy
Creating a Pattern Recognition Strategy Using the RSI in Python
Classical patterns such as double tops and double bottoms have been around for decades. We tend to apply them on the market price as we like to look at pure price action. What if we try them on transformations of prices? In this article, we will apply the pattern recognition tools of such configurations on a contrarian indicator named the relative strength index.
It is finally out! My newest book with O’Reilly Media on candlestick pattern recognition is now available on Amazon! The book features a huge number of classic and modern candlestick patterns as it dwelves into the realm of technical analysis with different trading strategies. The book comes with its own GitHub and is dynamic in nature as it is continuously updated and questions are answered on the O’Reilly platform.
Mastering Financial Pattern Recognition
Amazon.com: Mastering Financial Pattern Recognition eBook : Kaabar, Sofien: Kindle Storewww.amazon.com
The Relative Strength Index
First introduced by J. Welles Wilder Jr., the RSI is one of the most popular and versatile technical indicators. Mainly used as a contrarian indicator where extreme values signal a reaction that can be exploited. Typically, we use the following steps to calculate the default RSI:
Calculate the change in the closing prices from the previous ones.
Separate the positive net changes from the negative net changes.
Calculate a smoothed moving average on the positive net changes and on the absolute values of the negative net changes.
Divide the smoothed positive changes by the smoothed negative changes. We will refer to this calculation as the Relative Strength — RS.
Apply the normalization formula shown below for every time step to get the RSI.
The above chart shows the hourly values of the GBPUSD in black with the 13-period RSI. We can generally note that the RSI tends to bounce close to 25 while it tends to pause around 75. To code the RSI in Python, we need an OHLC array composed of four columns that cover open, high, low, and close prices.
def adder(data, times):
for i in range(1, times + 1):
new = np.zeros((len(data), 1), dtype = float)
data = np.append(data, new, axis = 1)return datadef deleter(data, index, times):
for i in range(1, times + 1):
data = np.delete(data, index, axis = 1)return data
def jump(data, jump):
data = data[jump:, ]
return datadef ma(data, lookback, close, where):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = (data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
data = jump(data, lookback)
return datadef ema(data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
data = ma(data, lookback, what, where)data[lookback + 1, where] = (data[lookback + 1, what] * alpha) + (data[lookback, where] * beta)for i in range(lookback + 2, len(data)):
try:
data[i, where] = (data[i, what] * alpha) + (data[i - 1, where] * beta)
except IndexError:
pass
return datadef rsi(data, lookback, close, where):
data = adder(data, 5)
for i in range(len(data)):
data[i, where] = data[i, close] - data[i - 1, close]
for i in range(len(data)):
if data[i, where] > 0:
data[i, where + 1] = data[i, where]
elif data[i, where] < 0:
data[i, where + 2] = abs(data[i, where])
lookback = (lookback * 2) - 1 # From exponential to smoothed
data = ema(data, 2, lookback, where + 1, where + 3)
data = ema(data, 2, lookback, where + 2, where + 4)data[:, where + 5] = data[:, where + 3] / data[:, where + 4]
data[:, where + 6] = (100 - (100 / (1 + data[:, where + 5])))data = deleter(data, where, 6)
data = jump(data, lookback)return dataThe Double Top / Double Bottom Pattern
Patterns are everywhere around us. We like them because we have an idea on what they mean or what to expect from them. In its pure form, a pattern is a recurring configuration familiar to the mind or the algorithm. In the financial markets industry, we can add that it gives us a clue on the possible direction of the market after it appears. This is to say that financial patterns are desired when analyzing the charts in order to forecast the direction of the market. Among patterns are what we call double tops and double bottoms.
A double top is a bearish configuration characterized by having two peaks before the market breaks the neckline between them and heads lower.
A double bottom is a bullish configuration characterized by having two troughs before the market surpasses the neckline between them and heads higher.
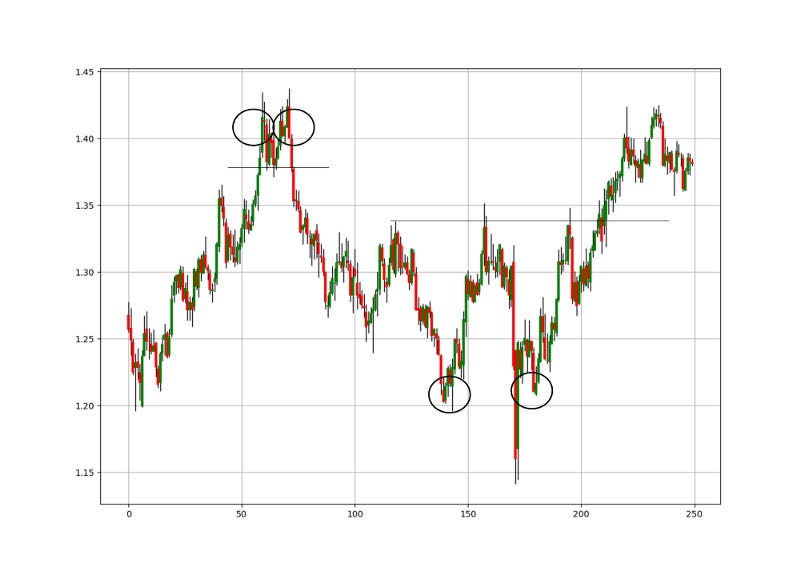
The neckline is the support or resistance level between the two peaks/troughs that must be broken to validate the pattern. The chart above shows the weekly values on the AUDUSD. The two circles on the left show a double top configuration with the neckline in black. Once the neckline is broken, the pattern is validated and we can expect a bearish reaction. Note that the neckline is most likely the low between the two peaks.
The two circles on the right also show a doubletop pattern but a less obvious one. Some might even say it resembles other reversal patterns (Which will be covered in future articles).
The chart above shows the weekly values on the GBPUSD. The two circles on the left show a double top configuration with the neckline in black. The two circles on the right represent a double bottom pattern.
In the article, we will use the pattern recognition algorithm to search for the two above patterns but not on the market price, but rather on the RSI.
Creating the Strategy
Let us review the trading conditions that we will be making for the patterns to be valid on the RSI:
For a double bottom: The RSI must dip below the oversold area (30), then it must surpass it, followed by another dip below it but above the first dip, and finally, it must surpass the oversold area (30).
For a double top: The RSI must surpass the overbought area (70), then it must dip below it, followed by another surpass above it but below the first surpass, and finally, it must dip below the overbought area (70).
I have chosen to simplify the rules and not include the neckline but consider the re-integration of the extreme levels as simply the final condition. You can try to code the original condition by simply following the intuition that for a double bottom, the final condition must be higher than the maximum level between the two troughs and as for the double top, the final condition must be lower than the minimum level between the two peaks.
The above chart shows the weekly EURUSD values with the 13-period RSI. Let us apply the following signal function to find the patterns.
# Indicator Parameters
lookback = 13
lower_barrier = 30
upper_barrier = 70
width = 60def signal(Data, indicator, width, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
try:
if Data[i, indicator] < lower_barrier:
for a in range(i + 1, i + width):
# First trough
if Data[a, indicator] > lower_barrier:
for r in range(a + 1, a + width):
if Data[r, indicator] < lower_barrier and \
Data[r, indicator] >= Data[i, indicator] and Data[r, indicator] - Data[i, indicator] < 3:
for s in range(r + 1, r + width):
# Second trough
if Data[s, indicator] > lower_barrier:
Data[s, buy] = 1
break
else:
break
else:
break
else:
break
else:
break
except IndexError:
passfor i in range(len(Data)):
try:
if Data[i, indicator] > upper_barrier:
for a in range(i + 1, i + width):
# First trough
if Data[a, indicator] < upper_barrier:
for r in range(a + 1, a + width):
if Data[r, indicator] > upper_barrier and \
Data[r, indicator] <= Data[i, indicator] and Data[i, indicator] - Data[r, indicator] < 3:
for s in range(r + 1, r + width):
# Second trough
if Data[s, indicator] < upper_barrier:
Data[s, sell] = -1
break
else:
break
else:
break
else:
break
else:
break
except IndexError:
pass
return Datamy_data = adder(my_data, 10)
my_data = rsi(my_data, lookback, 3, 4)
my_data = signal(my_data, 4, width, 6, 7)The above signal chart shows the trades generated on the EURUSD weekly values following the conditions given.
The function can be optimized to reflect the trader’s preferences of the patterns. The width variables is how far the algorithm will search within two peaks or troughs.
Evaluating the Strategy
Having had the signals, we now know when the algorithm would have placed its buy and sell orders, meaning, that we have an approximate replica of the past where can can control our decisions with no hindsight bias. We have to simulate how the strategy would have done given our conditions. This means that we need to calculate the returns and analyze the performance metrics. Let us see a neutral metric that can give us somewhat a clue on the predictability of the indicator or the strategy. For this study, we will use the Signal Quality metric.
The signal quality is a metric that resembles a fixed holding period strategy. It is simply the reaction of the market after a specified time period following the signal. Generally, when trading, we tend to use a variable period where we open the positions and close out when we get a signal on the other direction or when we get stopped out (either positively or negatively).
Sometimes, we close out at random time periods. Therefore, the signal quality is a very simple measure that assumes a fixed holding period and then checks the market level at that time point to compare it with the entry level. In other words, it measures market timing by checking the reaction of the market after a specified time period.
# Choosing a Holding Period for a trend-following strategy
period = 3def signal_quality(Data, closing, buy, sell, period, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
if Data[i, buy] == 1:
Data[i + period, where] = Data[i + period, closing] - Data[i, closing]
if Data[i, sell] == -1:
Data[i + period, where] = Data[i, closing] - Data[i + period, closing]
except IndexError:
pass
return Data# Applying the Signal Quality Function
my_data = signal_quality(my_data, 3, 6, 7, period, 8)positives = my_data[my_data[:, 8] > 0]
negatives = my_data[my_data[:, 8] < 0]# Calculating Signal Quality
signal_quality = len(positives) / (len(negatives) + len(positives))print('Signal Quality = ', round(signal_quality * 100, 2), '%')# Output Signal Quality USDCAD = 53.67%A signal quality of 53.67% means that on 100 trades, we tend to see a profitable result in 53 of the cases without taking into account transaction costs.
If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.