Creating an Innovative Pull-Back Trading Strategy.
Coding the Pull-Back Trading Strategy on the Relative Strength Index.
The Relative Strength Index is a known contrarian indicator but can also be used to confirm a new trend by other methods such as a pull-back. We are used to using this technique on the market price, but it can also be used on the technical indicators. This article discusses the method in detail.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret. The RSI is notably used in many ways, among them:
The extremes strategy: Where we search for overbought an oversold levels to initiate contrarian trades. The idea is that an overbought market has a high reading on the RSI signifying too much bullish momentum and a possible correction or even a reversal may take place. Similarly, an oversold market has a low reading on the RSI signifying too much bearish momentum and a possible correction or even a reversal may take place.
The divergence strategy: When there is an established trend, the overall direction does not move linearly with regards to magnitude and force, meaning that when a market is rising, its momentum strength is not stable. At the beginning it is usually strong but by profit taking and lower convictions, the market starts to lose some strength, thus, continuing to rise but struggling to do so. This is where we see a bearish divergence on the RSI. A divergence signifies the trend’s exhaustion and may signal a correction or even a reversal. Visually, a bearish divergence is when we see the market making higher highs while the RSI is making lower highs. Similarly, a bullish divergence is when we see the market making lower lows while the RSI is making higher lows.
The fact that it is famous, contributes to the efficacy of the RSI. This is because the more traders and portfolio managers look at the indicator, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index through the following function, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
def rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback)
return DataWe need to define the primal manipulation functions first in order to use the RSI’s function on OHLC data arrays.
# The function to add a certain number of columns
def adder(Data, times):
for i in range(1, times + 1):
z = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, z, axis = 1)
return Data
# The function to deleter a certain number of columns
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a certain number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return DataNow, we will see a less known strategy on the RSI which is generally used as a confirmation of the new expected reversal. It can be considered as an entry technique on the extremes strategy.
Creating the Pull-Back Strategy
The pull-back method is a very known technique in the world of trading, it is based on the fact that after a breakout, the market will stabilize before continuing higher due to profit-taking and increased orders in the contrarian direction in anticipation that the support/resistance level will hold. This generally provides a good entry level for the trades in the right direction. Below is an illustration of a pull-back.
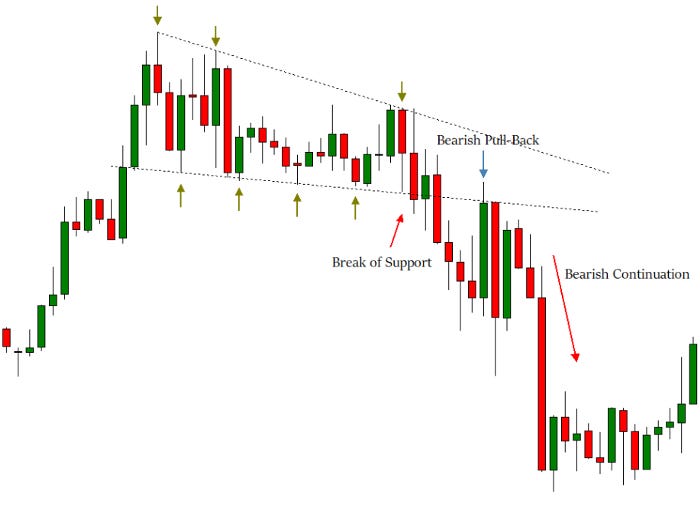
Another example can be an exit of a triangular configuration such as the below. The market has broken its descending support outlined with the green upwards pointing arrows, then tried coming back but found resistance at the same descending support line which is now resistance, to finally continue the drop. This is a perfect example of a pull-back.
The idea of the strategy is to apply this method on the famous technical indicator, the Relative Strength Index. It will be easier to code as we have objective barriers already which we call oversold and overbought levels.
An oversold level is typically below 30 and refers to a state of the market where selling activity was a bit extreme. Therefore, whenever the RSI surpasses the 30 level after being below it, and then retraces back close to it, a bullish signal is generated.
An overbought level is typically above 70 and refers to a state of the market where buying activity was a bit extreme. Therefore, whenever the RSI breaks the 70 level after being above it, and then retraces back close to it, a bearish signal is generated.
Basically, we will be applying the exact same pull-back method on the Relative Strength Index and using the signals as directional confirmation.
lookback = 13
upper_barrier = 70
lower_barrier = 30
margin = 2
def signal(Data, rsi_column, buy, sell):
Data = adder(Data, 20)
for i in range(len(Data)):
if Data[i, rsi_column] >= lower_barrier and Data[i, rsi_column] <= lower_barrier + margin and Data[i - 1, rsi_column] > lower_barrier and Data[i - 2, rsi_column] < lower_barrier:
Data[i, buy] = 1
elif Data[i, rsi_column] <= upper_barrier and Data[i, rsi_column] >= upper_barrier - margin and Data[i - 1, rsi_column] < upper_barrier and Data[i - 2, rsi_column] > upper_barrier:
Data[i, sell] = -1
return Data
# The margin variable is the maximum distance for the pull-back to be valid. A margin of 2 and a lower barrier of 30 means that that the RSI can retrace back to between 30 and 32 and the event can still be considered a pull-backThe chart above shows the one signal generated by the algorithm. It can be seen that the moment the RSI has fulfilled all the conditions, a bearish signal around the top has been generated.
Many optimization and modifications can be added to the algorithm such as:
Tweaking the margin variable so that more pull-backs are taken into account. We should not make this variable too high so that we remain in the spirit of the strategy.
Adding the condition that looks more into the past so that slow pull-backs are considered.
Tweaking the RSI’s lookback period even though the default values are recommended as a very short RSI has unreliable pull-back signals due to the short life between the extremes.
Adding a moving average break confirmation signal.
The pull-back method is theoretically a laggard compared to the extremes and the barrier exit ones but is the best regarding to entry optimization and realization of the reaction due to the fact that the extremes can last a long time and the barrier exit can provide an expensive entry level. Also, the pull-back method can help avoid false breakouts.
Conclusion & Important Disclaimer
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing Back-testing results should lead the reader to explore more herself the strategy and work on it more. That way you can share with me your better strategy and we will get rich together.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.