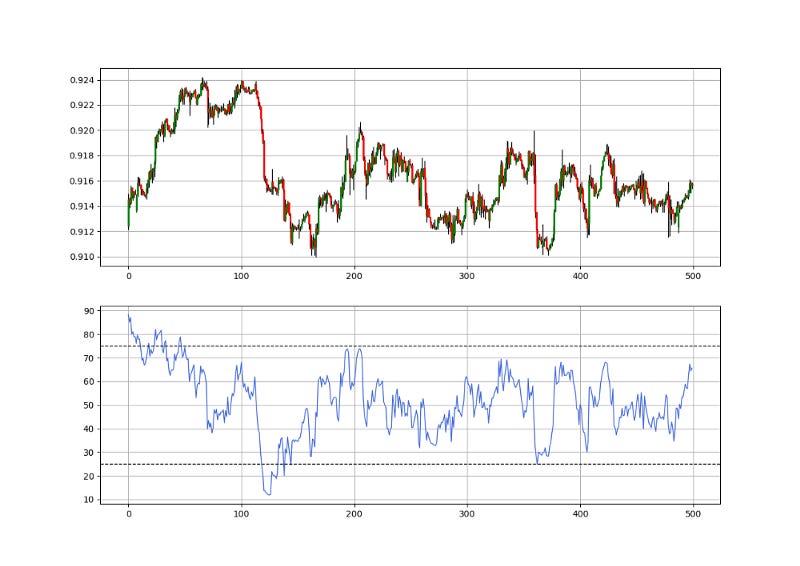
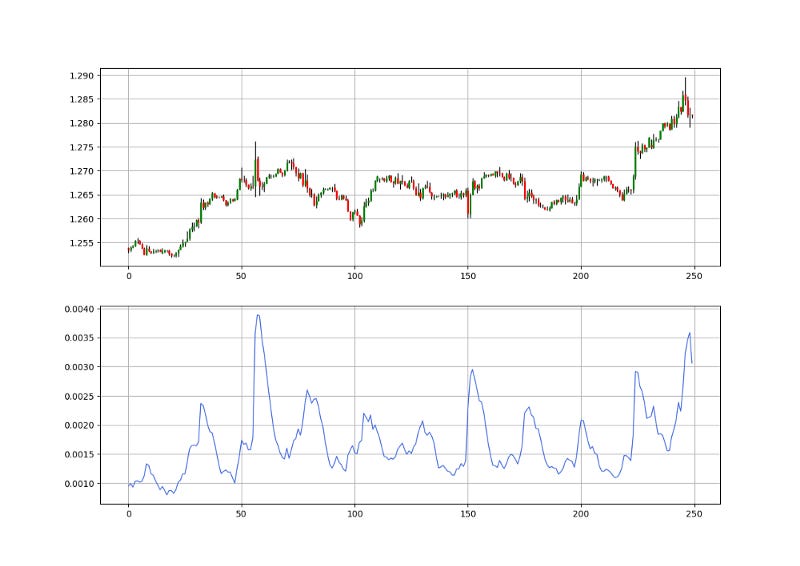
Creating a Volatility-Adjusted Momentum Indicator in Python.
Coding and Trading a Volatility-Adjusted RSI in Python.
Structured indicators are the result of fusing two or more together to form a weighted or adjusted indicator that takes into account more variables. For example, we know that there is a Stochastic-RSI indicator which combines the two formulas together in an attempt to improve the signals, this article discusses the creation of an RSI-ATR indicator which adjusts the RSI for the average true range, a measure of volatility.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below Amazon link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Relative Strength Index
The RSI is without a doubt the most famous momentum indicator out there, and this is to be expected as it has many strengths especially in ranging markets. It is also bounded between 0 and 100 which makes it easier to interpret.
Also, the fact that it is famous, contributes to its potential.
This is because the more traders and portfolio managers look at the RSI, the more people will react based on its signals and this in turn can push market prices. Of course, we cannot prove this idea, but it is intuitive as one of the basis of Technical Analysis is that it is self-fulfilling.
The RSI is calculated using a rather simple way. We first start by taking price differences of one period. This means that we have to subtract every closing price from the one before it. Then, we will calculate the smoothed average of the positive differences and divide it by the smoothed average of the negative differences. The last calculation gives us the Relative Strength which is then used in the RSI formula to be transformed into a measure between 0 and 100.
To calculate the Relative Strength Index, we need an OHLC array (not a data frame). This means that we will be looking at an array of 4 columns. The function for the Relative Strength Index is therefore:
# The function to add a number of columns inside an array
def adder(Data, times):
for i in range(1, times + 1):
new_col = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, new_col, axis = 1)
return Data# The function to delete a number of columns starting from an index
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return Data# Example of adding 3 empty columns to an array
my_ohlc_array = adder(my_ohlc_array, 3)# Example of deleting the 2 columns after the column indexed at 3
my_ohlc_array = deleter(my_ohlc_array, 3, 2)# Example of deleting the first 20 rows
my_ohlc_array = jump(my_ohlc_array, 20)# Remember, OHLC is an abbreviation of Open, High, Low, and Close and it refers to the standard historical data filedef ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return Datadef ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return Datadef rsi(Data, lookback, close, where, width = 1, genre = 'Smoothed'):
# Adding a few columns
Data = adder(Data, 7)
# Calculating Differences
for i in range(len(Data)):
Data[i, where] = Data[i, close] - Data[i - width, close]
# Calculating the Up and Down absolute values
for i in range(len(Data)):
if Data[i, where] > 0:
Data[i, where + 1] = Data[i, where]
elif Data[i, where] < 0:
Data[i, where + 2] = abs(Data[i, where])
# Calculating the Smoothed Moving Average on Up and Down
absolute values
if genre == 'Smoothed':
lookback = (lookback * 2) - 1 # From exponential to smoothed
Data = ema(Data, 2, lookback, where + 1, where + 3)
Data = ema(Data, 2, lookback, where + 2, where + 4)
if genre == 'Simple':
Data = ma(Data, lookback, where + 1, where + 3)
Data = ma(Data, lookback, where + 2, where + 4)
# Calculating the Relative Strength
Data[:, where + 5] = Data[:, where + 3] / Data[:, where + 4]
# Calculate the Relative Strength Index
Data[:, where + 6] = (100 - (100 / (1 + Data[:, where + 5])))
# Cleaning
Data = deleter(Data, where, 6)
Data = jump(Data, lookback) return DataThe Average True Range Indicator
We sometimes measure volatility using the Average True Range. Although the ATR is considered a lagging indicator, it gives some insights as to where volatility is right now and where has it been last period (day, week, month, etc.). But before that, we should understand how the True Range is calculated (the ATR is just the average of that calculation).
The true range is simply the greatest of the three price differences:
High — Low
| High — Previous close |
| Previous close — Low |
Once we have gotten the maximum out of the above three, we simply take an average of n periods of the true ranges to get the Average True Range. Generally, since in periods of panic and price depreciation we see volatility go up, the ATR will most likely trend higher during these periods, similarly in times of steady uptrends or downtrends, the ATR will tend to go lower.
One should always remember that this indicator is lagging and therefore has to be used with extreme caution. Below is the function code that calculates the ATR. Make sure you have an OHLC array of historical data.
def atr(Data, lookback, high, low, close, where, genre = 'Smoothed'):
# Adding the required columns
Data = adder(Data, 1)
# True Range Calculation
for i in range(len(Data)):
try:
Data[i, where] = max(Data[i, high] - Data[i, low],
abs(Data[i, high] - Data[i - 1, close]),
abs(Data[i, low] - Data[i - 1, close]))
except ValueError:
pass
Data[0, where] = 0
if genre == 'Smoothed':
# Average True Range Calculation
Data = ema(Data, 2, lookback, where, where + 1)
if genre == 'Simple':
# Average True Range Calculation
Data = ma(Data, lookback, where, where + 1)
# Cleaning
Data = deleter(Data, where, 1)
Data = jump(Data, lookback) return DataThe RSI/ATR Indicator
The idea is to divide the values of the RSI by the ATR so that we find a measure adjusted by the recent volatility. However, by doing so, we will find unbounded values, which is why we will apply the RSI formula on the values we find. Therefore, to calculate the RSI/ATR indicator, we follow these steps:
Calculate a 14-period RSI on the market price.
Calculate a 14-period ATR on the market price.
Divide the RSI by the ATR values.
Calculate a 14-period RSI on the results from the last step.
lookback = 14
upper_barrier = 70
lower_barrier = 30# Calculating a 14-period RSI
my_data = rsi(my_data, lookback, 3, 4)# Calculating a 14-period ATR
my_data = atr(my_data, lookback, 1, 2, 3, 5)# Adding a few empty columns
my_data = adder(my_data, 10)# Dividing the RSI by the ATR
my_data[:, 6] = my_data[:, 4] / my_data[:, 5]# Calculating the RSI on the values from the last step
my_data = rsi(my_data, lookback, 6, 7)# Cleaning
my_data = deleter(my_data, 4, 3)The RSI/ATR resembles the regular RSI but takes into account some volatility measures. It is of course not a perfect indicator nor is it proven that it is better than the RSI but it is very optimizable as it has more variables and is an uncharted territory.
def signal(Data, rsi_col, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, rsi_col] <= lower_barrier and Data[i - 1, buy] == 0 and Data[i - 2, buy] == 0 and Data[i - 3, buy] == 0:
Data[i, buy] = 1
elif Data[i, rsi_col] >= upper_barrier and Data[i - 1, sell] == 0 and Data[i - 2, sell] == 0 and Data[i - 3, sell] == 0:
Data[i, sell] = -1
return Datamy_data = signal(my_data, 4, 6, 7)The signal charts show the trades taken whenever the 14-period RSI/ATR reaches 30 (For a long position) and 70 (For a short position).
If you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Conclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.