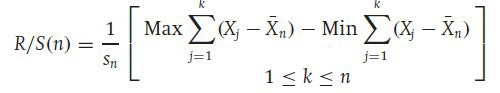Creating a Fractal Trading Strategy for Advanced Contrarian Signals
Using the Fractal Indicator With Moving Averages to Trade the Markets
The efficient market hypothesis fails to account for the many anomalies and recurring exploitable patterns within financial assets. This is why active portfolio management is still the dominant party when compared to passive investing. Financial markets are not perfectly random, they are random-like, i.e. they exhibit a low signal-to-noise ratio.
In other words, it is hard to predict the markets and even harder to be consistently profitable. However, the word hard does not mean impossible. We will develop an indicator that uses a formula close to the Rescaled Range calculation which is often related to fractal mathematics, albeit simpler in nature.
After all, we do not need to overcomplicate things to understand how the market moves. We will try to combine the signals from this Fractal Indicator with moving averages so as to filter and keep the good ones.
Knowledge must be accessible to everyone. This is why, from now on, a purchase of either one of my new books “Contrarian Trading Strategies in Python” or “Trend Following Strategies in Python” comes with free PDF copies of my first three books (Therefore, purchasing one of the new books gets you 4 books in total). The two new books listed above feature a lot of advanced indicators and strategies with a GitHub page. You can use the below link to purchase one of the two books (Please specify which one and make sure to include your e-mail in the note).
Pay Kaabar using PayPal.Me
Go to paypal.me/sofienkaabar and type in the amount. Since it’s PayPal, it’s easy and secure. Don’t have a PayPal…www.paypal.com
The Fractal Indicator
Chaos Theory is a very complex mathematical field that has the job of explaining the effects of very small factors. The Butterfly Effect comes to mind when thinking of Chaos Theory. The mentioned effect is the phenomenon where insignificant factors can lead to extreme changes. A chaotic system is an environment that alternates between predictability and randomness, and this is the closest explanation that we have so far for the financial markets.
The efficient market hypothesis fails to thoroughly explain the market dynamics and it is better for now to stick to real trading results and historical performances as a judge for whether markets are predictable or not. The early experiments with Chaos Theory occurred with Edward Lorenz, a meteorologist who wanted to simulate weather sequences by incorporating different variables such as temperature and wind speed. Lorenz noticed that whenever he made tiny adjustments in the variables, the final results were extremely different. This was the first proof of the Butterfly Effect which is one of the pillars of Chaos Theory.
The assumption in Chaos Theory vis-a-vis financial markets is that price is the last thing to change and that the current price is the most important information.
As stated above, Lorenz has proven that chaotic systems are impacted by the slightest changes in their variables. This makes us think about the time where if a certain financial information does not get released or is a bit different, where would the market trade? Emotions and independent situations all contribute to determining the market price as well. Imagine if a giant hedge fund changed its mind from buying the EUR versus the USD at the last minute and that this information has gone out to the public. Many traders who would have wanted to ride the giant bullish trend along the hedge fund would have eventually changed their minds and this could actually have caused the EURUSD price to go down in value. The reason I am talking about Chaos Theory is because the indicator I am showing below uses a formula related to this field. Even though the financial applications of Chaos Theory remain vague and a little unbacked, it should not stop us from trying out new things. With that being said, we can start designing our Fractal Indicator.
British hydrologist Harold Edwin Hurst introduced a measure of variability of time series across the period of time analyzed. This measure is called the Rescaled Range Analysis which is the basis of our Fractal Indicator. Here is how to calculate Rescaled Range:
The Rescaled Range formula is very interesting as it takes into account the volatility (S), the mean (X-bar), and the range of the data to analyze its properties. What the above formula says is that, we have to calculate the range between the mini ranges of the maximum and minimum values and then divide them by the Standard Deviation, which in this case is the proxy for volatility.
As I am a perpetual fan of do-it-yourself and tweak-it-yourself, I have modified the formula to have the following sense which we will later see together in a step-by-step method:
Incorporating the highs and the lows could give us a clearer picture on volatility, which is why we will first calculate an exponential moving average on both the lows and highs for the previous X period and then calculate their respective standard deviation i.e. volatility. Next, we will calculate the first range where we will subtract the current high from the average high measured by the exponential moving average in the first step and then do the same thing with the low. After that, we will calculate a rolling maximum for the first range (the high minus its average) and a rolling minimum for the second range (the low minus its average). Then, we subtract the the high rolling maximum from the low rolling minimum before rescaling by dividing the result by the average between the two standard deviations calculated above for the highs and lows.
This is all done using the following function that requires an OHLC array, but first, we have to define the primal manipulation functions which will allow us to modify the arrays:
# The function to add a certain number of columns
def adder(Data, times):
for i in range(1, times + 1):
z = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, z, axis = 1)return Data# The function to deleter a certain number of columns
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data# The function to delete a certain number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return DataNow, for the Fractal Indicator function:
def fractal_indicator(Data, high, low, ema_lookback, min_max_lookback, where):
# Adding a few empty columns
Data = adder(Data, 10)
# Calculating exponential moving averages
Data = ema(Data, 2, ema_lookback, high, where)
Data = ema(Data, 2, ema_lookback, low, where + 1)
# Calculating volatility
Data = volatility(Data, ema_lookback, high, where + 2)
Data = volatility(Data, ema_lookback, low, where + 3)
# Calculating ranges
Data[:, where + 4] = Data[:, high] - Data[:, where]
Data[:, where + 5] = Data[:, low] - Data[:, where + 1]for i in range(len(Data)):
try:
Data[i, where + 6] = max(Data[i - min_max_lookback + 1:i + 1, where + 4])
except ValueError:
pass
for i in range(len(Data)):
try:
Data[i, where + 7] = min(Data[i - min_max_lookback + 1:i + 1, where + 5])
except ValueError:
pass
Data[:, where + 8] = (Data[:, where + 2] + Data[:, where + 3]) / 2
Data[:, where + 9] = (Data[:, where + 6] - Data[:, where + 7]) / Data[:, where + 8]
Data = deleter(Data, 5, 9)
Data = jump(Data, min_max_lookback)
return DataThe moving average function will be found below in the article, it must be defined before applying the above function.
So, it becomes clear, the Fractal Indicator is simply a reformed version of the Rescaled Range formula created by Harold Hurst.
The variables that go into the Fractal Indicator’s function are:
ema_lookback = 21 # The lookback on the moving averages
min_max_lookback = 13 # The lookback on the normalization
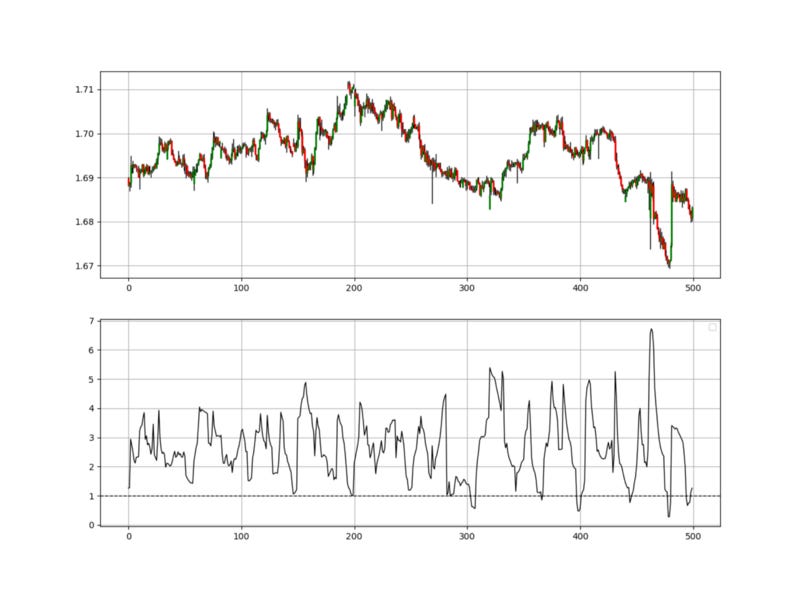
barrier = 1 # The threshold of market inflectionIn the above plot, we see a Fractal Indicator with 21-period exponential moving average and a 13-period normalization function, therefore, Fractal Indicator(21, 13). The idea on how to get signals from this indicator is this simple condition:
Whenever the indicator is showing a reading close 1 or below it, a structural break may be in place and a small reversal is likely.
Check out my weekly market sentiment report to understand the current positioning and to estimate the future direction of several major markets through complex and simple models working side by side. Find out more about the report through this link that covers the analysis between 07/08/2022 and 14/08/2022:
Coalescence Report 7th August — 14th August 2022
THIS IS A FREE SAMPLE GIVEN TO FREE SUBSCRIBERS THIS WEEK. IF YOU WANT TO REGULARLY HAVE THIS REPORT, MAKE SURE TO…coalescence.substack.com
Moving Averages
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
As the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
To code the simple moving average, we can follow this syntax in Python while making sure we have defined the primal manipulation functions also seen below:
def ma(Data, lookback, close, where):
Data = adder(Data, 1)for i in range(len(Data)):
try:Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())except IndexError:
pass# Cleaning
Data = jump(Data, lookback)return DataAnother even more dynamic moving average is the exponential one. Its idea is to give more weight to the more recent values so that it reduces the lag between the price and the average.
Notice how the exponential moving average is closer to prices than the simple one when the trend is strong. This is because it gives more weight to the latest values so that the average does not stay very far. To code a function in Python that outputs this type of average, you can use the below snippet:
def ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return DataCombining the Strategy
The idea here is to know what is the signal being given by the Fractal Indicator.
This can be answered by creating a moving average to filter the trend. Here is how:
If the Fractal Indicator is showing a value of 1 or below while the market is below its 200-period simple moving average, but a the same time below the close 8 bars from the current close, then the signal is bullish. These conditions are required to force a contrarian reaction.
If the Fractal Indicator is showing a value of 1 or below while the market is above its 200-period simple moving average, but a the same time above the close 8 bars from the current close, then the signal is bearish. These conditions are required to force a contrarian reaction.
def signal(Data, close, fractal_col, ma_col, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, fractal_col] <= barrier and Data[i, close] < Data[i, ma_col] and Data[i - 1, buy] == 0 and \
Data[i, close] < Data[i - 8, close]:
Data[i, buy] = 1
elif Data[i, fractal_col] <= barrier and Data[i, close] > Data[i, ma_col] and Data[i - 1, sell] == 0 and \
Data[i, close] > Data[i - 8, close]:
Data[i, sell] = -1
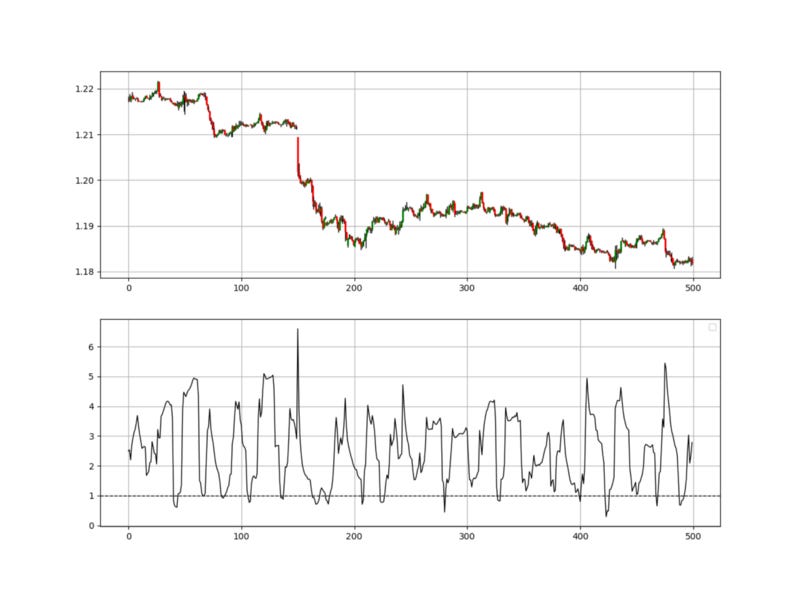
return DataThe above chart shows how the signals are generated. Whenever we see an extreme on the Fractal Indicator while having the other conditions, we tend to have a reversion to the mean.
The strategy works better in low trending markets or ranging ones since such markets are characterised by mean-reversion. The above chart shows the signals generated on the GBPCHF.
The structure of the strategy can be summed up in the below code:
ema_lookback = 21
min_max_lookback = 13
ma_lookback = 200
barrier = 1# Coding the Fractal Indicator
my_data = fractal_indicator(my_data, 1, 2, ema_lookback, min_max_lookback, 5)# Coding the Simple Moving Average
my_data= ma(my_data, ma_lookback, 3, 6)# Coding the signal function
my_data= signal(my_data, 3, 5, 6, 7, 8)If you want to see how to create all sorts of algorithms yourself, feel free to check out Lumiwealth. From algorithmic trading to blockchain and machine learning, they have hands-on detailed courses that I highly recommend.
Learn Algorithmic Trading with Python Lumiwealth
Learn how to create your own trading algorithms for stocks, options, crypto and more from the experts at Lumiwealth. Click to learn more
Summary
To sum up, what I am trying to do is to simply contribute to the world of objective technical analysis which is promoting more transparent techniques and strategies that need to be back-tested before being implemented. This way, technical analysis will get rid of the bad reputation of being subjective and scientifically unfounded.
I recommend you always follow the the below steps whenever you come across a trading technique or strategy:
Have a critical mindset and get rid of any emotions.
Back-test it using real life simulation and conditions.
If you find potential, try optimizing it and running a forward test.
Always include transaction costs and any slippage simulation in your tests.
Always include risk management and position sizing in your tests.
Finally, even after making sure of the above, stay careful and monitor the strategy because market dynamics may shift and make the strategy unprofitable.