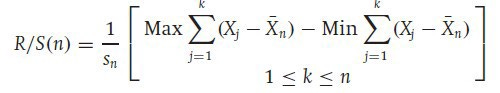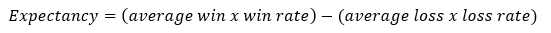Creating a Fractal Trading Strategy for Advanced Contrarian Signals.
Using the Fractal Indicator With Moving Averages to Trade the Markets.
The efficient market hypothesis fails to account for the many anomalies and recurring exploitable patterns within financial assets. This is why active portfolio management is still the dominant party when compared to passive investing. Financial markets are not perfectly random, they are random-like, i.e. they exhibit a low signal-to-noise ratio.
In other words, it is hard to predict the markets and even harder to be consistently profitable. However, the word hard does not mean impossible. We will develop an indicator that uses a formula close to the Rescaled Range calculation which is often related to fractal mathematics, albeit simpler in nature.
After all, we do not need to overcomplicate things to understand how the market moves. We will try to combine the signals from this Fractal Indicator with moving averages so as to filter and keep the good ones.
I have just published a new book after the success of my previous one “New Technical Indicators in Python”. It features a more complete description and addition of structured trading strategies with a GitHub page dedicated to the continuously updated code. If you feel that this interests you, feel free to visit the below link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Fractal Indicator
Chaos Theory is a very complex mathematical field that has the job of explaining the effects of very small factors. The Butterfly Effect comes to mind when thinking of Chaos Theory. The mentioned effect is the phenomenon where insignificant factors can lead to extreme changes. A chaotic system is an environment that alternates between predictability and randomness, and this is the closest explanation that we have so far for the financial markets.
The efficient market hypothesis fails to thoroughly explain the market dynamics and it is better for now to stick to real trading results and historical performances as a judge for whether markets are predictable or not. The early experiments with Chaos Theory occurred with Edward Lorenz, a meteorologist who wanted to simulate weather sequences by incorporating different variables such as temperature and wind speed. Lorenz noticed that whenever he made tiny adjustments in the variables, the final results were extremely different. This was the first proof of the Butterfly Effect which is one of the pillars of Chaos Theory.
The assumption in Chaos Theory vis-à-vis financial markets is that price is the last thing to change and that the current price is the most important information.
As stated above, Lorenz has proven that chaotic systems are impacted by the slightest changes in their variables. This makes us think about the time where if a certain financial information does not get released or is a bit different, where would the market trade? Emotions and independent situations all contribute to determining the market price as well. Imagine if a giant hedge fund changed its mind from buying the EUR versus the USD at the last minute and that this information has gone out to the public. Many traders who would have wanted to ride the giant bullish trend along the hedge fund would have eventually changed their minds and this could actually have caused the EURUSD price to go down in value. The reason I am talking about Chaos Theory is because the indicator I am showing below uses a formula related to this field. Even though the financial applications of Chaos Theory remain vague and a little unbacked, it should not stop us from trying out new things. With that being said, we can start designing our Fractal Indicator.
British hydrologist Harold Edwin Hurst introduced a measure of variability of time series across the period of time analyzed. This measure is called the Rescaled Range Analysis which is the basis of our Fractal Indicator. Here is how to calculate Rescaled Range:
The Rescaled Range formula is very interesting as it takes into account the volatility (S), the mean (X-bar), and the range of the data to analyze its properties. What the above formula says is that, we have to calculate the range between the mini ranges of the maximum and minimum values and then divide them by the Standard Deviation, which in this case is the proxy for volatility.
As I am a perpetual fan of do-it-yourself and tweak-it-yourself, I have modified the formula to have the following sense which we will later see together in a step-by-step method:
Incorporating the highs and the lows could give us a clearer picture on volatility, which is why we will first calculate an exponential moving average on both the lows and highs for the previous X period and then calculate their respective standard deviation i.e. volatility. Next, we will calculate the first range where we will subtract the current high from the average high measured by the exponential moving average in the first step and then do the same thing with the low. After that, we will calculate a rolling maximum for the first range (the high minus its average) and a rolling minimum for the second range (the low minus its average). Then, we subtract the the high rolling maximum from the low rolling minimum before rescaling by dividing the result by the average between the two standard deviations calculated above for the highs and lows.
This is all done using the following function that requires an OHLC array, but first, we have to define the primal manipulation functions which will allow us to modify the arrays:
# The function to add a certain number of columns
def adder(Data, times):
for i in range(1, times + 1):
z = np.zeros((len(Data), 1), dtype = float)
Data = np.append(Data, z, axis = 1) return Data
# The function to deleter a certain number of columns
def deleter(Data, index, times):
for i in range(1, times + 1):
Data = np.delete(Data, index, axis = 1)
return Data
# The function to delete a certain number of rows from the beginning
def jump(Data, jump):
Data = Data[jump:, ]
return DataNow, for the Fractal Indicator function:
def fractal_indicator(Data, high, low, ema_lookback, min_max_lookback, where):
# Adding a few empty columns
Data = adder(Data, 10)
# Calculating exponential moving averages
Data = ema(Data, 2, ema_lookback, high, where)
Data = ema(Data, 2, ema_lookback, low, where + 1)
# Calculating volatility
Data = volatility(Data, ema_lookback, high, where + 2)
Data = volatility(Data, ema_lookback, low, where + 3)
# Calculating ranges
Data[:, where + 4] = Data[:, high] - Data[:, where]
Data[:, where + 5] = Data[:, low] - Data[:, where + 1]
for i in range(len(Data)):
try:
Data[i, where + 6] = max(Data[i - min_max_lookback + 1:i + 1, where + 4])
except ValueError:
pass
for i in range(len(Data)):
try:
Data[i, where + 7] = min(Data[i - min_max_lookback + 1:i + 1, where + 5])
except ValueError:
pass
Data[:, where + 8] = (Data[:, where + 2] + Data[:, where + 3]) / 2
Data[:, where + 9] = (Data[:, where + 6] - Data[:, where + 7]) / Data[:, where + 8]
Data = deleter(Data, 5, 9)
Data = jump(Data, min_max_lookback)
return DataThe moving average function will be found below in the article, it must be defined before applying the above function.
So, it becomes clear, the Fractal Indicator is simply a reformed version of the Rescaled Range formula created by Harold Hurst.
The variables that go into the Fractal Indicator’s function are:
ema_lookback = 21 # The lookback on the moving averages
min_max_lookback = 13 # The lookback on the normalization
barrier = 1 # The threshold of market inflectionIn the above plot, we see a Fractal Indicator with 21-period exponential moving average and a 13-period normalization function, therefore, Fractal Indicator(21, 13). The idea on how to get signals from this indicator is this simple condition:
Whenever the indicator is showing a reading close 1 or below it, a structural break may be in place and a small reversal is likely.
If you are also interested by more technical indicators and using Python to create strategies, then my best-selling book on Technical Indicators may interest you:
Moving Averages
Moving averages help us confirm and ride the trend. They are the most known technical indicator and this is because of their simplicity and their proven track record of adding value to the analyses. We can use them to find support and resistance levels, stops and targets, and to understand the underlying trend. This versatility makes them an indispensable tool in our trading arsenal.
As the name suggests, this is your plain simple mean that is used everywhere in statistics and basically any other part in our lives. It is simply the total values of the observations divided by the number of observations. Mathematically speaking, it can be written down as:
To code the simple moving average, we can follow this syntax in Python while making sure we have defined the primal manipulation functions also seen below:
def ma(Data, lookback, close, where):
Data = adder(Data, 1)
for i in range(len(Data)):
try:
Data[i, where] = (Data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
# Cleaning
Data = jump(Data, lookback)
return DataAnother even more dynamic moving average is the exponential one. Its idea is to give more weight to the more recent values so that it reduces the lag between the price and the average.
Notice how the exponential moving average is closer to prices than the simple one when the trend is strong. This is because it gives more weight to the latest values so that the average does not stay very far. To code a function in Python that outputs this type of average, you can use the below snippet:
def ema(Data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
# First value is a simple SMA
Data = ma(Data, lookback, what, where)
# Calculating first EMA
Data[lookback + 1, where] = (Data[lookback + 1, what] * alpha) + (Data[lookback, where] * beta)
# Calculating the rest of EMA
for i in range(lookback + 2, len(Data)):
try:
Data[i, where] = (Data[i, what] * alpha) + (Data[i - 1, where] * beta)
except IndexError:
pass
return DataCombining the Strategy
The idea here is to know what is the signal being given by the Fractal Indicator. This can be answered by creating a moving average to filter the trend. Here is how:
If the Fractal Indicator is showing a value of 1 or below while the market is below its 200-period simple moving average, but a the same time below the close 8 bars from the current close, then the signal is bullish. These conditions are required to force a contrarian reaction.
If the Fractal Indicator is showing a value of 1 or below while the market is above its 200-period simple moving average, but a the same time above the close 8 bars from the current close, then the signal is bearish. These conditions are required to force a contrarian reaction.
def signal(Data, close, fractal_col, ma_col, buy, sell):
Data = adder(Data, 10)
for i in range(len(Data)):
if Data[i, fractal_col] <= barrier and Data[i, close] < Data[i, ma_col] and Data[i - 1, buy] == 0 and \
Data[i, close] < Data[i - 8, close]:
Data[i, buy] = 1
elif Data[i, fractal_col] <= barrier and Data[i, close] > Data[i, ma_col] and Data[i - 1, sell] == 0 and \
Data[i, close] > Data[i - 8, close]:
Data[i, sell] = -1
return DataThe above chart shows how the signals are generated. Whenever we see an extreme on the Fractal Indicator while having the other conditions, we tend to have a reversion to the mean.
The strategy works better in low trending markets or ranging ones since such markets are characterized by mean-reversion. The above chart shows the signals generated on the GBPCHF.
The structure of the strategy can be summed up in the below code:
ema_lookback = 21
min_max_lookback = 13
ma_lookback = 200
barrier = 1
# Coding the Fractal Indicator
my_data = fractal_indicator(my_data, 1, 2, ema_lookback, min_max_lookback, 5)
# Coding the Simple Moving Average
my_data= ma(my_data, ma_lookback, 3, 6)
# Coding the signal function
my_data= signal(my_data, 3, 5, 6, 7, 8)The Framework of Strategy Back-testing
Having had the signals, we now know when the algorithm would have placed its buy and sell orders, meaning, that we have an approximate replica of the past where can can control our decisions with no hindsight bias. We have to simulate how the strategy would have done given our conditions. This means that we need to calculate the returns and analyze the performance metrics. This section will try to cover the essentials and provide a framework. We can first start with the simplest measure of all, the profit and loss statement. When we back-test our system, we want to see whether it has made money or lost money. After all, it is a game of wealth. This can be done by calculating the gains and losses, the gross and net return, as well as charting the equity plot which is simply the time series of our balance given a perfect algorithm that initiates buy and sell orders based on the strategy. Before we see that, we have to make sure of the following since we want a framework that fits everywhere:
The above table says that we need to have the indicator or the signal generator at column 4 or 5 (Remember, indexing at Python starts at zero). The buy signal (constant = 1) at the column indexed at 6, and the sell short signal (constant = -1) at the column indexed at 7. This ensures the remainder of the code below works how it should work. The reason for this is that on an OHLC data, we have already the first 4 columns occupied, leaving us 1 or 2 columns to place our Indicators, before having two signal columns. Using the deleter function seen above can help you achieve this order in case the indicators occupy more than 2 columns.
The first step into building the Equity Curve is to calculate the profits and losses from the individual trades we are taking. For simplicity reasons, we can consider buying and selling at closing prices. This means that when we get the signal from the indicator or the pattern on close, we initiate the trade on the close until getting another signal where we exit and initiate the new trade. In real life, we do this mainly on the next open, but generally in FX, there is not a huge difference. The code to be defined for the profit/loss columns is the below:
def holding(Data, buy, sell, buy_return, sell_return):for i in range(len(Data)):
try:
if Data[i, buy] == 1:
for a in range(i + 1, i + 1000):
if Data[a, buy] != 0 or Data[a, sell] != 0:
Data[a, buy_return] = (Data[a, 3] - Data[i, 3])
break
else:
continue
elif Data[i, sell] == -1:
for a in range(i + 1, i + 1000):
if Data[a, buy] != 0 or Data[a, sell] != 0:
Data[a, sell_return] = (Data[i, 3] - Data[a, 3])
break
else:
continue
except IndexError:
pass# Using the function
holding(my_data, 6, 7, 8, 9)This will give us columns 8 and 9 populated with the gross profit and loss results from the trades taken. Now, we have to transform them into cumulative numbers so that we calculate the Equity Curve. To do that, we use the below indexer function:
def indexer(Data, expected_cost, lot, investment):
# Charting portfolio evolution
indexer = Data[:, 8:10]
# Creating a combined array for long and short returns
z = np.zeros((len(Data), 1), dtype = float)
indexer = np.append(indexer, z, axis = 1)
# Combining Returns
for i in range(len(indexer)):
try:
if indexer[i, 0] != 0:
indexer[i, 2] = indexer[i, 0] - (expected_cost / lot)
if indexer[i, 1] != 0:
indexer[i, 2] = indexer[i, 1] - (expected_cost / lot)
except IndexError:
pass
# Switching to monetary values
indexer[:, 2] = indexer[:, 2] * lot
# Creating a portfolio balance array
indexer = np.append(indexer, z, axis = 1)
indexer[:, 3] = investment
# Adding returns to the balance
for i in range(len(indexer)):
indexer[i, 3] = indexer[i - 1, 3] + (indexer[i, 2])
indexer = np.array(indexer)
return np.array(indexer)# Using the function for a 0.1 lot strategy on $10,000 investment
expected_cost = 0.5 * (lot / 10000) # 0.5 pip spread
investment = 10000
lot = 10000
equity_curve = indexer(my_data, expected_cost, lot, investment)The below code is used to generate the chart. Note that the indexer function nets the returns using the estimated transaction cost, hence, the equity curve that would be charted is theoretically net of fees.
plt.plot(equity_curve[:, 3], linewidth = 1, label = 'EURUSD)
plt.grid()
plt.legend()
plt.axhline(y = investment, color = 'black’, linewidth = 1)
plt.title(’Strategy’, fontsize = 20)Now, it is time to start evaluating the performance using other measures.
I will present quickly the main ratios and metrics before presenting a full performance function that outputs them all together. Hence, the below discussions are mainly informational, if you are interested by the code, you can find it at the end.
Hit ratio = 42.28 % # Simulated RatioThe Hit Ratio is extremely easy to use. It is simply the number of winning trades over the number of the trades taken in total. For example, if we have 1359 trades over the course of 5 years and we have been profitable in 711 of them , then our hit ratio (accuracy) is 711/1359 = 52.31%.
The Net Profit is simply the last value in the Equity Curve net of fees minus the initial balance. It is simply the added value on the amount we have invested in the beginning.
Net profit = $ 1209.4 # Simulated ProfitThe net return measure is your return on your investment or equity. If you started with $1000 and at the end of the year, your balance shows $1300, then you would have made a healthy 30%.
Net Return = 30.01% # Simulated ReturnA quick glance on the Average Gain across the trades and the Average Loss can help us manage our risks better. For example, if our average gain is $1.20 and our average loss is $4.02, then we know that something is not right as we are risking way too much money for way too little gain.
Average Gain = $ 56.95 per trade # Simulated Average Gain
Average Loss = $ -41.14 per trade # Simulated Average LossFollowing that, we can calculate two measures:
The theoretical risk-reward ratio: This is the desired ratio of average gains to average losses. A ratio of 2.0 means we are targeting twice as much as we are risking.
The realized risk-reward ratio: This is the actual ratio of average gains to average losses. A ratio of 0.75 means we are targeting three quarters of what we are risking.
Theoretical Risk Reward = 2.00 # Simulated Ratio
Realized Risk Reward = 0.75 # Simulated RatioThe Profit Factor is a relatively quick and straightforward method to compute the profitability of the strategy. It is calculated as the total gross profit over the total gross loss in absolute values, hence, the interpretation of the profit factor (also referred to as the profitability index in the jargon of corporate finance) is how much profit is generated per $1 of loss. The formula for the profit factor is:
Profit factor = 1.34 # Simulated Profit FactorExpectancy is a flexible measure presented by the well-known Laurent Bernut that is composed of the average win/loss and the hit ratio. It provides the expected profit or loss on a dollar figure weighted by the hit ratio. The win rate is what we refer to as the hit ratio in the below formula, and through that, the loss ratio is 1 — hit ratio.
Expectancy = $ 1.33 per trade # Simulated ExpectancyAnother interesting measure is the number of trades. This is simply to understand the frequency of the trades we have.
Trades = 3697 # Simulated NumberNow, we are ready to have all of the above metrics shown at the same time. After calculating the indexer function, we can use the below performance function to give us the metrics we need:
def performance(indexer, Data, name):
# Profitability index
indexer = np.delete(indexer, 0, axis = 1)
indexer = np.delete(indexer, 0, axis = 1)
profits = []
losses = []
np.count_nonzero(Data[:, 7])
np.count_nonzero(Data[:, 8])
for i in range(len(indexer)):
if indexer[i, 0] > 0:
value = indexer[i, 0]
profits = np.append(profits, value)
if indexer[i, 0] < 0:
value = indexer[i, 0]
losses = np.append(losses, value)
# Hit ratio calculation
hit_ratio = round((len(profits) / (len(profits) + len(losses))) * 100, 2)
realized_risk_reward = round(abs(profits.mean() / losses.mean()), 2)
# Expected and total profits / losses
expected_profits = np.mean(profits)
expected_losses = np.abs(np.mean(losses))
total_profits = round(np.sum(profits), 3)
total_losses = round(np.abs(np.sum(losses)), 3)
# Expectancy
expectancy = round((expected_profits * (hit_ratio / 100)) \
- (expected_losses * (1 - (hit_ratio / 100))), 2)
# Largest Win and Largest Loss
largest_win = round(max(profits), 2)
largest_loss = round(min(losses), 2) # Total Return
indexer = Data[:, 10:12]
# Creating a combined array for long and short returns
z = np.zeros((len(Data), 1), dtype = float)
indexer = np.append(indexer, z, axis = 1)
# Combining Returns
for i in range(len(indexer)):
try:
if indexer[i, 0] != 0:
indexer[i, 2] = indexer[i, 0] - (expected_cost / lot)
if indexer[i, 1] != 0:
indexer[i, 2] = indexer[i, 1] - (expected_cost / lot)
except IndexError:
pass
# Switching to monetary values
indexer[:, 2] = indexer[:, 2] * lot
# Creating a portfolio balance array
indexer = np.append(indexer, z, axis = 1)
indexer[:, 3] = investment
# Adding returns to the balance
for i in range(len(indexer)):
indexer[i, 3] = indexer[i - 1, 3] + (indexer[i, 2])
indexer = np.array(indexer)
total_return = (indexer[-1, 3] / indexer[0, 3]) - 1
total_return = total_return * 100
print('-----------Performance-----------', name)
print('Hit ratio = ', hit_ratio, '%')
print('Net profit = ', '$', round(indexer[-1, 3] - indexer[0, 3], 2))
print('Expectancy = ', '$', expectancy, 'per trade')
print('Profit factor = ' , round(total_profits / total_losses, 2))
print('Total Return = ', round(total_return, 2), '%')
print('')
print('Average Gain = ', '$', round((expected_profits), 2), 'per trade')
print('Average Loss = ', '$', round((expected_losses * -1), 2), 'per trade')
print('Largest Gain = ', '$', largest_win)
print('Largest Loss = ', '$', largest_loss)
print('')
print('Realized RR = ', realized_risk_reward)
print('Minimum =', '$', round(min(indexer[:, 3]), 2))
print('Maximum =', '$', round(max(indexer[:, 3]), 2))
print('Trades =', len(profits) + len(losses))
# Using the function
performance(equity_curve, my_data, 'EURUSD)This should give us something like the below:
-----------Performance----------- EURUSD
Hit ratio = 42.28 %
Net profit = $ 1209.4
Expectancy = $ 0.33 per trade
Profit factor = 1.01
Total Return = 120.94 %
Average Gain = $ 56.95 per trade
Average Loss = $ -41.14 per trade
Largest Gain = $ 347.5
Largest Loss = $ -311.6Realized RR = 1.38
Minimum = $ -1957.6
Maximum = $ 4004.2
Trades = 3697# All of the above are simulated results and do not reflect the presented strategy or indicatorConclusion & Important Disclaimer
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing Back-testing results should lead the reader to explore more herself the strategy and work on it more. That way you can share with me your better strategy and we will get rich together.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.