Trend following strategies rely on confirmation techniques to detect as early as possible a new trend. This article discusses a strategy on the RSI and the SuperTrend.
I have just released a new book after the success of my previous one “The Book of Trading Strategies”. It features advanced trend-following indicators and strategies with a GitHub page dedicated to the continuously updated code. Also, this book features the original colors after having optimized for printing costs. If you feel that this interests you, feel free to visit the below Amazon link, or if you prefer to buy the PDF version, you could contact me on LinkedIn.
The Relative Strength Index
First introduced by J. Welles Wilder Jr., the RSI is one of the most popular and versatile technical indicators. Mainly used as a contrarian indicator where extreme values signal a reaction that can be exploited. Typically, we use the following steps to calculate the default RSI:
Calculate the change in the closing prices from the previous ones.
Separate the positive net changes from the negative net changes.
Calculate a smoothed moving average on the positive net changes and on the absolute values of the negative net changes.
Divide the smoothed positive changes by the smoothed negative changes. We will refer to this calculation as the Relative Strength — RS.
Apply the normalization formula shown below for every time step to get the RSI.
The above chart shows the hourly values of the GBPUSD in black with the 13-period RSI. We can generally note that the RSI tends to bounce close to 25 while it tends to pause around 75. To code the RSI in Python, we need an OHLC array composed of four columns that cover open, high, low, and close prices.
def adder(data, times):
for i in range(1, times + 1):
new = np.zeros((len(data), 1), dtype = float)
data = np.append(data, new, axis = 1) return datadef deleter(data, index, times):
for i in range(1, times + 1):
data = np.delete(data, index, axis = 1) return data
def jump(data, jump):
data = data[jump:, ]
return datadef ma(data, lookback, close, where):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = (data[i - lookback + 1:i + 1, close].mean())
except IndexError:
pass
data = jump(data, lookback)
return datadef ema(data, alpha, lookback, what, where):
alpha = alpha / (lookback + 1.0)
beta = 1 - alpha
data = ma(data, lookback, what, where) data[lookback + 1, where] = (data[lookback + 1, what] * alpha) + (data[lookback, where] * beta) for i in range(lookback + 2, len(data)):
try:
data[i, where] = (data[i, what] * alpha) + (data[i - 1, where] * beta)
except IndexError:
pass
return datadef rsi(data, lookback, close, where):
data = adder(data, 5)
for i in range(len(data)):
data[i, where] = data[i, close] - data[i - 1, close]
for i in range(len(data)):
if data[i, where] > 0:
data[i, where + 1] = data[i, where]
elif data[i, where] < 0:
data[i, where + 2] = abs(data[i, where])
lookback = (lookback * 2) - 1 # From exponential to smoothed
data = ema(data, 2, lookback, where + 1, where + 3)
data = ema(data, 2, lookback, where + 2, where + 4) data[:, where + 5] = data[:, where + 3] / data[:, where + 4]
data[:, where + 6] = (100 - (100 / (1 + data[:, where + 5]))) data = deleter(data, where, 6)
data = jump(data, lookback) return dataThe SuperTrend
The first concept we should understand before creating the SuperTrend indicator is volatility. We sometimes measure volatility using the average true range. Although the ATR is considered a lagging indicator, it gives some insights as to where volatility is right now and where has it been last period (day, week, month, etc.). But before that, we should understand how the true range is calculated (the ATR is just the average of that calculation). The true range is simply the greatest of the three price differences:
High — Low
| High — Previous close |
| Previous close — Low |
Once we have gotten the maximum out of the above three, we simply take an average of n periods of the true ranges to get the average true range. Generally, since in periods of panic and price depreciation we see volatility go up, the ATR will most likely trend higher during these periods, similarly in times of steady uptrends or downtrends, the ATR will tend to go lower.
One should always remember that this indicator is lagging and therefore has to be used with extreme caution. Below is the function code that calculates the ATR. Make sure you have an OHLC array of historical data.
def atr(data, lookback, high, low, close, where):
data = adder(data, 1)
for i in range(len(data)):
try:
data[i, where] = max(data[i, high] - data[i, low], abs(data[i, high] - data[i - 1, close]), abs(data[i, low] - data[i - 1, close]))
except ValueError:
pass
data[0, where] = 0
data = ema(data, 2, (lookback * 2) - 1, where, where + 1) data = deleter(data, where, 1)
data = jump(data, lookback)
return dataNow that we have understood what the ATR is and how to calculate it, we can proceed further with the SuperTrend indicator. The indicator seeks to provide entry and exit levels for trend followers. You can think of it as a moving average or an MACD. Its uniqueness is its main advantage and although its calculation method is much more complicated than the other two indicators, it is intuitive in nature and not that hard to understand. Basically, we have two variables to choose from. The ATR lookback and the multiplier’s value. The former is just the period used to calculated the ATR while the latter is generally an integer (usually 2 or 3).
The first thing to do is to average the high and low of the price bar, then we will either add or subtract the average with the selected multiplier multiplied by the ATR as shown in the above formulas. This will give us two arrays, the basic upper band and the basic lower band which form the first building blocks in the SuperTrend indicator. The next step is to calculate the final upper band and the final lower band using the below formulas.
It may seem complicated but most of these conditions are repetitive and in any case, I will provide the Python code below so that you can play with the function and optimize it to your trading preferences. Finally, using the previous two calculations, we can find the SuperTrend.
def supertrend(data, multiplier, high, low, close, atr_col, where):
data = adder(data, 6)
for i in range(len(data)):
data[i, where] = (data[i, high] + data[i, low]) / 2
data[i, where + 1] = data[i, where] + (multiplier * data[i, atr_col])
data[i, where + 2] = data[i, where] - (multiplier * data[i, atr_col])
for i in range(len(data)):
if i == 0:
data[i, where + 3] = 0
else:
if (data[i, where + 1] < data[i - 1, where + 3]) or (data[i - 1, close] > data[i - 1, where + 3]):
data[i, where + 3] = data[i, where + 1]
else:
data[i, where + 3] = data[i - 1, where + 3]
for i in range(len(data)):
if i == 0:
data[i, where + 4] = 0
else:
if (data[i, where + 2] > data[i - 1, where + 4]) or (data[i - 1, close] < data[i - 1, where + 4]):
data[i, where + 4] = data[i, where + 2]
else:
data[i, where + 4] = data[i - 1, where + 4]
for i in range(len(data)):
if i == 0:
data[i, where + 5] = 0
elif (data[i - 1, where + 5] == data[i - 1, where + 3]) and (data[i, close] <= data[i, where + 3]):
data[i, where + 5] = data[i, where + 3]
elif (data[i - 1, where + 5] == data[i - 1, where + 3]) and (data[i, close] > data[i, where + 3]):
data[i, where + 5] = data[i, where + 4]
elif (data[i - 1, where + 5] == data[i - 1, where + 4]) and (data[i, close] >= data[i, where + 4]):
data[i, where + 5] = data[i, where + 4]
elif (data[i - 1, where + 5] == data[i - 1, where + 4]) and (data[i, close] < data[i, where + 4]):
data[i, where + 5] = data[i, where + 3]
data = deleter(data, where, 5) data = jump(data, 1)
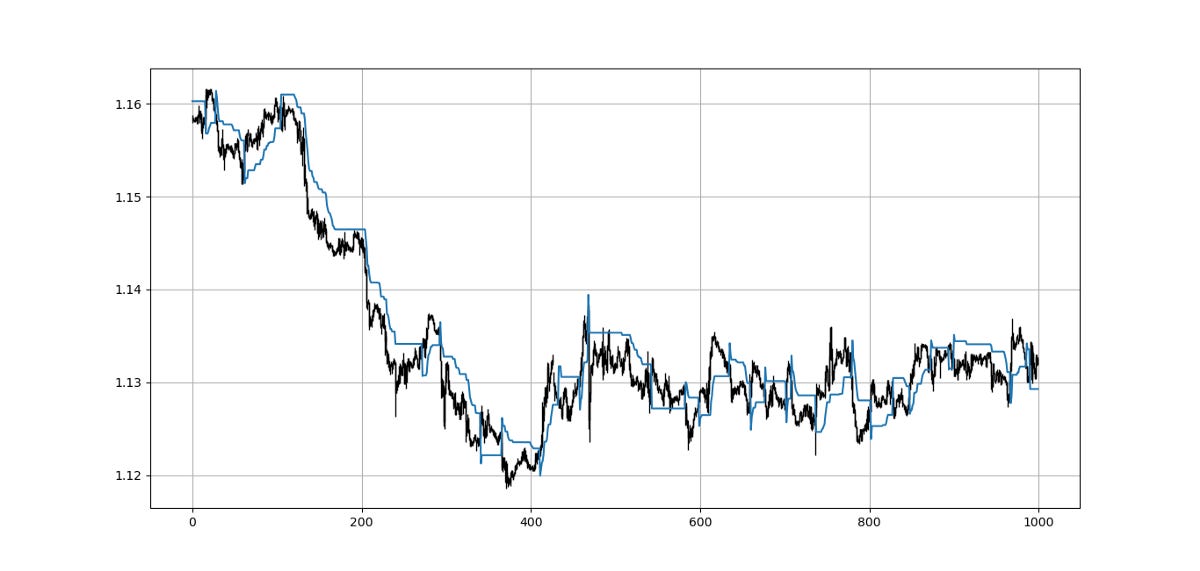
return dataThe above chart shows the hourly values of the EURUSD with a 10-period SuperTrend (represented by the ATR period) and a multiplier of 3. The way we should understand the indicator is that when it goes above the market price, we should be looking to short and when it goes below the market price, we should be looking to go long as we anticipate a bullish trend. Remember that the SuperTrend is a trend-following indicator. The aim here is to capture trends at the beginning and to close out when they are over.
Creating the Strategy
The strategy relies on signals from the SuperTrend and confirmation from the RSI. Here are the trading conditions keeping in mind that the parameters and the lookbacks must be tweaked in order to minimize lag and optimize the triggers:
Long (Buy) whenever the market surpasses the SuperTrend while the RSI is above 50.
Short (Sell) whenever the market breaks the SuperTrend while the RSI is below 50.
def signal(data, close, rsi_column, supertrend_column, buy, sell):
data = adder(data, 5)
for i in range(len(data)):
if data[i, rsi_column] > 50 and data[i, close] > data[i, supertrend_column] and data[i - 1, close] < data[i - 1, supertrend_column]:
data[i, buy] = 1
if data[i, rsi_column] < 50 and data[i, close] < data[i, supertrend_column] and data[i - 1, close] > data[i - 1, supertrend_column]:
data[i, sell] = -1
return dataConclusion
Remember to always do your back-tests. You should always believe that other people are wrong. My indicators and style of trading may work for me but maybe not for you.
I am a firm believer of not spoon-feeding. I have learnt by doing and not by copying. You should get the idea, the function, the intuition, the conditions of the strategy, and then elaborate (an even better) one yourself so that you back-test and improve it before deciding to take it live or to eliminate it. My choice of not providing specific Back-testing results should lead the reader to explore more herself the strategy and work on it more.
To sum up, are the strategies I provide realistic? Yes, but only by optimizing the environment (robust algorithm, low costs, honest broker, proper risk management, and order management). Are the strategies provided only for the sole use of trading? No, it is to stimulate brainstorming and getting more trading ideas as we are all sick of hearing about an oversold RSI as a reason to go short or a resistance being surpassed as a reason to go long. I am trying to introduce a new field called Objective Technical Analysis where we use hard data to judge our techniques rather than rely on outdated classical methods.