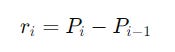Calculating Parkinson’s Volatility in Python
How to Code Parkinson’s Volatility For Time Series Analysis
Parkinson’s volatility is a measure of historical volatility that utilizes the high and low prices of a financial instrument over a given period. It is considered to be more efficient than the standard close-to-close volatility estimator because it incorporates the intraday price range, capturing more information about price movements within the day.
This article presents this volatility measure in detail and shows how to code a rolling calculation on time series using Python.
Understanding Parkinson’s Volatility
Before discussing complex volatility models, it is always recommended to have a thorough understanding of the most basic volatility model (or calculation), that is the historical standard deviation. The standard deviation using the historical method is a common way to measure the volatility of a financial instrument based on past price data.
It quantifies the amount of variation or dispersion of a set of values. In finance, it typically measures the dispersion of daily returns around their mean. Follow these steps to calculate the standard deviation:
Calculate the returns using either the differencing (first function) or the log method (second function).
Calculate the average (mean) of the returns:
Compute the variance of the daily returns:
The standard deviation is the square root of the variance:
Like any statistical measure, it has its advantages and disadvantages. The historical standard deviation is straightforward to compute. It requires basic statistical operations that can be easily implemented in spreadsheets and programming languages. It is a well-understood measure of variability and is easy to explain to stakeholders who may not have a deep statistical background. Many financial models and risk metrics (such as the Sharpe ratio) rely on standard deviation as a measure of risk.
For small sample sizes, the historical standard deviation tends to underestimate true volatility. This bias can lead to misleading conclusions about the risk of an asset. The method assumes that the underlying volatility of the asset is constant over the period being analyzed. In reality, volatility can change over time, making this assumption unrealistic.
Additionally, financial returns often exhibit fat tails (leptokurtosis) and skewness, meaning they do not follow a normal distribution. The standard deviation does not capture these characteristics, potentially underestimating risk.
Use the following code in Python to calculate a rolling 5-day measure of volatility on Nvidia’s daily returns:
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
def calculate_rolling_historical_volatility(data, window):
# Calculate returns (using the differencing method)
returns = data['Close'] - data['Close'].shift(1).dropna()
# Calculate the rolling standard deviation of the returns
rolling_volatility = returns.rolling(window=window).std()
# return a variable containing standard deviation measures
return rolling_volatility
# download the historical values of Nvidia
df = yf.download("NVDA", start = "2022-01-01", end = "2024-06-30")
# Define the rolling window size
window_size = 5
# apply the formula and get the volatility data frame
rolling_volatility = calculate_rolling_historical_volatility(df, window=window_size)
# plot volatility across time
plt.plot(rolling_volatility, color = 'black', label = '5-period historical standard deviation')
plt.legend()
plt.grid()
plt.axhline(y = np.mean(rolling_volatility), color = 'red', linestyle = 'dashed')Parkinson’s volatility, as proposed by Michael Parkinson in 1980, provides a more precise estimate of historical volatility by incorporating intraday price information, specifically the daily high and low prices.
By considering the high and low prices, Parkinson’s volatility captures the range of prices throughout the day, providing a more comprehensive view of volatility.
The formula for Parkinson’s volatility is:
Parkinson’s volatility provides a more accurate measure of volatility compared to standard deviation using only closing prices because it incorporates the high and low prices, which capture the intraday price movements more comprehensively.
This makes it particularly useful for markets or instruments with significant intraday volatility.
If you want to see more of my work, you can visit my website for the books catalogue by simply following this link:
Calculating Parkinson’s Volatility in Python
Let’s now use Python to calculate Parkinson’s volatility. We will use the same example (i.e. Nvidia’s daily returns with a lookback period of 5):
import numpy as np
import matplotlib.pyplot as plt
import yfinance as yf
import math
def parkinson_volatility(price_data, window_size = 5, periods = 252, clean = True):
rs = (1.0 / (4.0 * math.log(2.0))) * ((price_data["High"] / price_data["Low"]).apply(np.log)) ** 2.0
def f(v):
return (periods * v.mean()) ** 0.5
result = rs.rolling(window = window_size, center = False).apply(func = f)
if clean:
return result.dropna()
else:
return
# download the historical values of Nvidia
df = yf.download("NVDA", start = "2022-01-01", end = "2024-06-30")
# Define the rolling window size
window_size = 5
# apply the formula and get the volatility data frame
rolling_volatility = parkinson_volatility(df)
# plot volatility across time
plt.plot(rolling_volatility, color = 'black', label = '5-period Parkinson`s volatility')
plt.legend()
plt.grid()
plt.axhline(y = np.mean(rolling_volatility), color = 'red', linestyle = 'dashed')The historical standard deviation is a useful and widely adopted measure of volatility due to its simplicity, ease of calculation, and general acceptance in the financial industry. However, its limitations, particularly in handling small sample sizes, non-stationary volatility, and the non-normal distribution of returns, suggest that it should be used with caution.
In situations where accuracy is paramount or sample sizes are small, alternative volatility measures like GARCH models may provide better risk assessments.
You can also check out my other newsletter The Weekly Market Sentiment Report that sends weekly directional views every weekend to highlight the important trading opportunities using a mix between sentiment analysis (COT report, put-call ratio, etc.) and rules-based technical analysis.
If you liked this article, do not hesitate to like and comment, to further the discussion!