An In-Depth Guide to Gaussian Process Regression

Training, Predicting, and Understanding Uncertainty with GPR

Sep 05, 2024

Gaussian process regression (GPR) is a powerful tool for regression tasks, particularly when uncertainty quantification is crucial. While it has limitations in terms of scalability, its flexibility and interpretability make it a valuable method in many scientific and engineering disciplines. This article shows how to create a time series algorithm based on this model.

Introduction to the Gaussian Process Regression

Gaussian process regression (GPR) is a non-parametric, Bayesian approach to regression that is particularly powerful for modeling uncertainty in predictions. Unlike traditional regression models that provide point estimates, GPR offers a probabilistic prediction, providing a full distribution over possible outcomes.

GPR is especially useful when dealing with small datasets, where its ability to model uncertainty is crucial.

A Gaussian Process (GP) is a collection of random variables, any finite number of which have a joint Gaussian distribution. GPs are used to define a distribution over functions, which allows us to model our belief about the function we want to learn.

There are two concepts to know with GPR (yes, just two for now). The mean function which defines the expected value of the said function at any point x, and the covariance function which describes how correlated the values of the function are at different points. Before seeing any data, our beliefs about the function are modeled as a GP with a prior mean function and covariance function. Once we have training data, we incorporate it using Bayes’ theorem to update our beliefs about the function. This involves combining the GP prior with the likelihood of the observed data.

The result is a new GP, the posterior distribution, which represents our updated beliefs after observing the data. This posterior GP is used to make predictions (if that makes any sense).

Kernel functions (or covariance functions) are at the heart of GPR. They define the shape of the functions we consider plausible. The can be as follows:

RBF: Also known as the Gaussian kernel, it is the most common choice due to its smoothness properties.
Matern: A more flexible kernel that can model rougher functions compared to the RBF.
Periodic: Useful for capturing repeating patterns in the data.

The choice of kernel affects the model’s ability to generalize and its interpretation of the data.

Training involves optimizing the hyperparameters of the kernel function by maximizing the marginal likelihood. This step adjusts the model to best fit the training data. Once the model is trained, predictions are made by evaluating the posterior distribution at new test points.

The main drawback of the GPR? Its performance relies heavily on the choice of the kernel function.

If you want to see more of my work, you can visit my website for the books catalogue by simply following this link:

Bookstore

Creating a GPR Algorithm in Python

Let’s create a simple experiment. We will import the data of the S&P 500 index, take its returns, train 90% of it using the GPR algorith, and test on the remaining 10%. Use the following code for the experiment:

import matplotlib.pyplot as plt
import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
import pandas_datareader as pdr

def data_preprocessing(data, num_lags, train_test_split):
    # Prepare the data for training
    x = []
    y = []
    for i in range(len(data) - num_lags):
        x.append(data[i:i + num_lags])
        y.append(data[i+ num_lags])
    # Convert the data to numpy arrays
    x = np.array(x)
    y = np.array(y)
    # Split the data into training and testing sets
    split_index = int(train_test_split * len(x))
    x_train = x[:split_index]
    y_train = y[:split_index]
    x_test = x[split_index:]
    y_test = y[split_index:]

    return x_train, y_train, x_test, y_test

def plot_train_test_values(window, train_window, y_train, y_test, y_predicted):
    prediction_window = window
    first = train_window
    second = window - first
    y_predicted = np.reshape(y_predicted, (-1, 1))
    y_test = np.reshape(y_test, (-1, 1))
    plotting_time_series = np.zeros((prediction_window, 3))
    plotting_time_series[0:first, 0] = y_train[-first:]
    plotting_time_series[first:, 1] = y_test[0:second, 0]
    plotting_time_series[first:, 2] = y_predicted[0:second, 0] 
    plotting_time_series[0:first, 1] = plotting_time_series[0:first, 1] / 0
    plotting_time_series[0:first, 2] = plotting_time_series[0:first, 2] / 0
    plotting_time_series[first:, 0] = plotting_time_series[first:, 0] / 0
    plt.plot(plotting_time_series[:, 0], label = 'Training data', color = 'black', linewidth = 2.5)
    plt.plot(plotting_time_series[:, 1], label = 'Test data', color = 'black', linestyle = 'dashed', linewidth = 2)
    plt.plot(plotting_time_series[:, 2], label = 'Predicted data', color = 'red', linewidth = 1)
    plt.axvline(x = first, color = 'black', linestyle = '--', linewidth = 1)
    plt.grid()
    plt.legend()

def calculate_accuracy(predicted_returns, real_returns):
    predicted_returns = np.reshape(predicted_returns, (-1, 1))
    real_returns = np.reshape(real_returns, (-1, 1))
    hits = sum((np.sign(predicted_returns)) == np.sign(real_returns))
    total_samples = len(predicted_returns)
    accuracy = hits / total_samples
    
    return accuracy[0] * 100

# Set the start and end dates for the data
start_date = '1970-01-01'
end_date   = '2024-06-01'

# Fetch S&P 500 price data
data = np.array((pdr.get_data_fred('SP500', start = start_date, end = end_date)).dropna())
data = np.reshape(data, (-1))
# importing the time series
data = np.diff(data[:,])

# Setting the hyperparameters
num_lags = 2
train_test_split = 0.90

# Creating the training and test sets
x_train, y_train, x_test, y_test = data_preprocessing(data, num_lags, train_test_split)

# Fitting the model
model = GaussianProcessRegressor()
model.fit(x_train, y_train)

# Predicting in-sample
y_predicted_train = np.reshape(model.predict(x_train), (-1, 1))

# Predicting out-of-sample
y_predicted = np.reshape(model.predict(x_test), (-1, 1))

# plotting
plot_train_test_values(100, 50, y_train, y_test, y_predicted)

# Performance evaluation
print('---')
print('Accuracy Train = ', round(calculate_accuracy(y_predicted_train, y_train), 2), '%')
print('Accuracy Test = ', round(calculate_accuracy(y_predicted, y_test), 2), '%')
print('Correlation In-Sample Predicted/Train = ', round(np.corrcoef(np.reshape(y_predicted_train, (-1)), y_train)[0][1], 3))
print('Correlation Out-of-Sample Predicted/Test = ', round(np.corrcoef(np.reshape(y_predicted, (-1)), np.reshape(y_test, (-1)))[0][1], 3))
print('---')

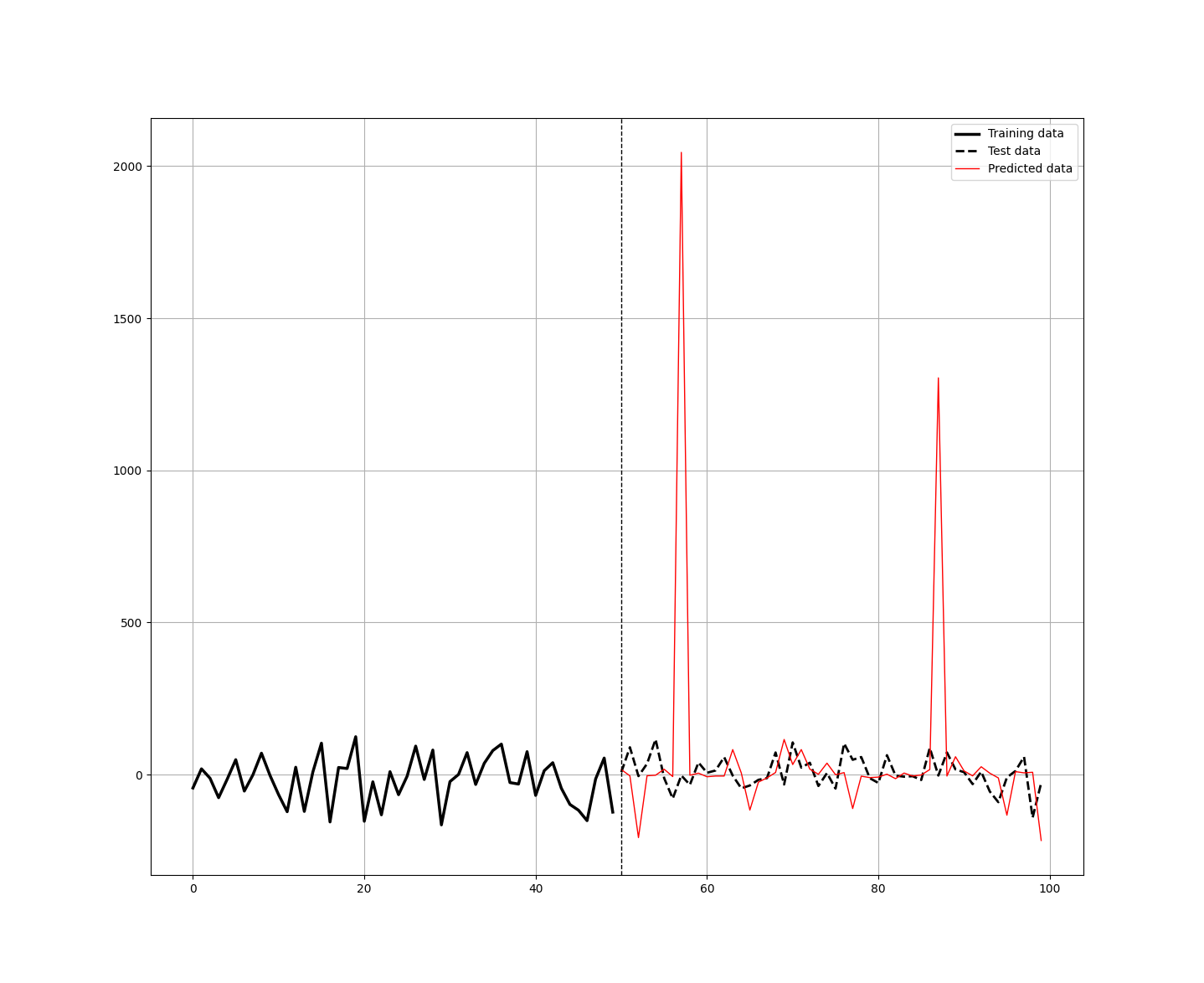
**Predictions (red) versus real values (dashed black)**

The results of the model were as follows:

---
Accuracy Train =  99.95 %
Accuracy Test =  48.37 %
Correlation In-Sample Predicted/Train =  1.0
Correlation Out-of-Sample Predicted/Test =  0.075
---

Clearly, this is a case of overfitting. How can we know that? Well, the training accuracy was 99.95% and the correlation between the predictions and the real values in the training set is 1.0. Additionally, the huge drop in accuracy from training to test is a major red flag for overfitting.

If we change a little the parameters to:

# Setting the hyperparameters
num_lags = 1
train_test_split = 0.80

We get the following results:

Accuracy Train =  64.19 %
Accuracy Test =  52.14 %
Correlation In-Sample Predicted/Train =  0.715
Correlation Out-of-Sample Predicted/Test =  -0.009

It seems that overfitting is considerably less when tweaking the parameters a little. The question is, how far should we tweak to eliminate overfitting? Here are some basic guidelines to help with this issue:

In GPR, the choice of kernel function plays a significant role in the model’s complexity. Using a simpler kernel can prevent the model from capturing too much noise. Avoid overly complex kernels that may lead to overfitting. In the kernel function, you can adjust hyperparameters like the length scale in the RBF kernel. A larger length scale can smooth out the model, reducing overfitting by discouraging it from fitting the noise in the data.

The parameter alpha in GaussianProcessRegressor acts as a regularization term, representing the variance of the noise. Increasing alpha can help the model to focus on the underlying trends rather than fitting the noise in the data.

Implementing cross-validation techniques (such as k-fold cross-validation) allows you to evaluate the model’s performance on different subsets of the data. This helps in tuning hyperparameters and selecting models that generalize better to unseen data. Sometimes, reducing the amount of training data can help avoid overfitting, especially if the data contains a lot of noise. However, this should be done cautiously, as it can also lead to underfitting.

Slightly perturbing the training data by adding noise or generating synthetic data can help the model learn more general features. This technique is more commonly used in deep learning but can be beneficial in preventing overfitting in other contexts as well.

You can also check out my other newsletter The Weekly Market Sentiment Report that sends weekly directional views every weekend to highlight the important trading opportunities using a mix between sentiment analysis (COT report, put-call ratio, etc.) and rules-based technical analysis.

The Weekly Market Sentiment Report

If you liked this article, do not hesitate to like and comment, to further the discussion!

All About Trading!

Discussion about this post