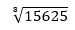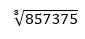Amazing Mental Math Techniques & Tricks
Performing Lightning Calculations in Our Minds
Mental math is one of those wonderful skills that are equally beneficial to us whether professionally or personally. Being able to make lightning calculations in our heads with accuracy is appealing and much easier than one might expect. Below are some tricks and shortcuts to perform mental operations.
Squaring Numbers Ending in 5.
When squaring two-digit numbers that end in 5, the result will have 25 as the last number while the left part will be n x (n+1). Hence, 85 x 85 = (8 x 9) and 25 giving us a result of 7225. Let’s try out some more examples:
15 x 15 = (1 x 2) and 25 = 225.
45 x 45 = (4 x 5) and 25 = 2025.
95 x 95 = (9 x 10) and 25 = 9025.
The above trick only works with two-digit squares that end in five.
Multiplication When Digits Add up to 10 With a Condition
The only conditions for the trick to work is to have a double-digit number that have both the right numbers equal to 10 and the left number is the same. The way to find the answer is to multiply the two right number and to do the same thing to the left numbers as we did in the first calculation, . Let’s check the below examples:
73 x 77 = (7 x 8) and (3 x 7) = 5621.
81 x 89 = (8 x 9) and (9 x 1) = 7209.
32 x 38 = (3 x 4) and (8 x 2) = 1216.
Multiplication By 5
This technique is as easy as it gets. To find the product of a number by 5, we simply multiply it by ten and then divide it by two.
76 x 5 = 76 x 10 = 760 / 2 = 380
135 x 5 = 135 x 10 = 1350 / 2 = 675
96 x 5 = 96 x 10 = 960 = 960 / 2 = 48
Multiplication by 11.
Multiplying by 11 is really simple. Here’s how. Consider 81 x 11. All we have to do is to add the two numbers composing the two-digit number, meaning 8 + 1 = 9. Then put it between the original numbers so that the result is 891. How about 42 x 11? In lightning speed, you’ll answer 462, which is correct. Let’s now see a slightly more complex example. What is 87 x 11? Well, 8 + 7 = 15, does that give us 8157? Not quite, we have to simply carry it so that we have 957. More examples:
56 x 11 = 616.
63 x 11 = 693.
25 x 11 = 275.
Multiplying Two-Digit Numbers Close to 100.
This is a very fun and easy technique. Multiplication of two-digit numbers is one of the advanced mental techniques that we should master in no time if we learn it right and practise it regularly. Let us take an example of the multiplication between 89 and 95. The first step we must do in our heads is calculate the distance between the two numbers from 100, meaning that we have to keep in our head 11 and 5. Next step is subtracting them from 100 giving us 84. Finally, we multiply them together, thus, multiplying 11 by 5 to get 55. The result is simply a combined number 8455. Here are more examples:
91 x 96 = (100–9–4) and (4 x 9) = 8736.
88 x 94 = (100–12–6) and (12 x 6) = 8272.
81 x 93 = (100–19–7) and (19 x 7) = 74 and 133, the key here is to add the 1 to 74, giving us 75 and 33. The answer is 7533.
Multiplying by 101 and by 111.
This quick and simple trick is used when you have a two-digit number multiplied by 101. The answer will be that same two-digit number written twice. Here are some examples:
28 x 101 = 2828.
74 x 101 = 7474.
36 x 101 = 3636.
To find the result of a two-digit number multiplied by 111, we simply follow this example. Consider 63 x 111. To find the answer, we sum the 6 and the 3 which gives us 9 then we write it two times between them. Therefore, the answer is 6993. If the two digits add up to more than 10, we carry the two numbers twice. Here’s an example to understand it more:
78 x 111 = 8658. Why? First, we add 7 + 8 giving us 15. Therefore, we have to carry the first time (65 instead of the usual 55 intuition like the above). Next we carry again, so, instead of starting with 7, we start with 8 which gives us 8658.
49 x 111 = 5439. Using the same intuition, we add 4 + 9 for a total of 13 which makes the middle numbers 43. As we carry the second time, we will start with 5. The end result is 5439.
Squaring Two-Digit Numbers
Here’s a very simple technique for squaring two-digit numbers. Suppose we want to find out 34 squared. How should we approach it? Well, first of all, we try to approach an easy number by subtracting or adding. If we want to approach 30, then we subtract 4. Now, we have to also add 4 on another spectrum. This gives us two numbers to keep in mind: 30 and 38. We multiply them together which is 38 x 10 x 3 = 1140. As a final step, we add to this final number the square of the subtracted/added number (which is 4), therefore 16 + 1140 = 1156. Let’s see some more examples:
18 x 18 = 20 x 16 = 320 + 4 = 3240
88 x 88 =90 x 86 = 7740 + 4 = 7744
46 x 46 = 50 x 42 = 42 x (100/2) = 2100 + 16 = 2116
199 x 199 = 200 x 198 = 39600 + 1 = 39601
Consider squaring the number 57. We will square the right digit 7 (because we will multiply 50 by 64). We will have 50 x 64 or 64 x 100 / 2 which is simply 3200. Finally, we add the square of the differenced value 7 which is 49, giving us a final result of 3249. Let’s look at more examples:
With a quick method for two-digit numbers between 50 and 59
Squaring 51 = 1 x 1 = 01 (We have to add the zero to the left when it’s a one-digit number. Now, we add 25 to 1, giving us 26. The result is therefore 2601.
Squaring 59 = 9 x 9 = 81. Now, we add 25 to 9, giving us 34. The result is therefore 3481.
Finding Cube Roots
When presented with a number and tasked to find its cube, you should drop the right three digits, then find the remaining number’s closest cube (by approximating the ones you memorize). Finally, the last number of the original number is used to find the right digit number of the cube. Math is always better with examples, let’s review and memorize first the cubing of numbers between 1 and 9:
Ignore 704 and focus on 592 for now giving us the closest cube 8 (because 8 x 8 x 8=512), so the first number of the square cube is 8. Now, we focus on the whole number 592704 and we take the digit that has a cube ending with that number, in this case it is 4 (because 4 x 4 x 4 = 64). The answer is 84.
Ignore 625 and focus on 15 for now giving us the closest cube 2 (because 2 x 2 x 2 = 8), so the first number of the square cube is 2. Now, we focus on the whole number 15625 and we take the digit that has a cube ending with that number, in this case it is 5 (because 5 x 5 x 5 = 125). The answer is 25.
Ignore 375 and focus on 857 for now giving us the closest cube 9 (because 9 x 9 x 9 = 729), so the first number of the square cube is 9. Now, we focus on the whole number 857375 and we take the digit that has a cube ending with that number, in this case it is 5 (because 5 x 5 x 5 = 125). The answer is 95.
Finding Percentages
When asked what is 6% of 2400 or 4.5% of 1800, it may seem intimidating but there are shortcuts that really help us either find the exact answer or approximate it. Let’s approach the first calculation.
6% x 2400 = What is 1% of 2400? Remove two zeroes and you’ll get 24. Now, all we have to do is multiply 24 by 6 which is a much simpler task. Simplifying the calculation to (20 x 6) + (6 x 4) gives us 144. So, 6% of 2400 is 144.
4.5% x 1800 = What is 1% of 1800? Well, the same method applies here to find 18. Now, the trick is to find 0.5%, which is simply 1% divided by two, hence, it is 9. So, 4.5% is 18 multiplied by 4 and added to 9. (18 x 4) + 9 = 81.
3% x 5000 = This one is very easy, 1% of 5000 is 50. Let’s multiply it by 3 and find 150 our answer.
1.1% x 1200 = This one is also easy. 1% of 1200 is 12. If we divide that by 10 to find the 0.1%, we get 1.2. Thus, 1.1% of 1200 is 13.2.
87% x 230 = What is 10% of 230? 23, right? Now, multiply it by 8 to get 184. What is 1% of 230? The answer is simply 2.3 which we have to multiply by 7 to get 16.1. The answer is 184 + 16.1 = 200.1
Fractions
One of the most basic tasks in Math is memorizing fractions. Some are easy such as 1/4 and 1/2 while some are difficult such as 3/7 and 5/9. However, there are patterns and shortcuts to follow that will help us calculate the fraction in lightning speed. Let’s start with the most common and interesting ones.
Fractions of 3 are known. Examples:
1 / 3 = 0.33333333333.
2 / 3 = 0.66666666666.
1 / 3 + 2 / 3 = 3 / 3 = 1.00
Fractions of 5 are even more known. Examples:
1 / 5 = 0.20
2 / 5 = 0.40
3 / 5 = 0.60
4 / 5 = 0.80
Fractions of 6 are a little more complicated. Examples:
1 / 6 = 0.16666666666.
2 / 6 = 1 / 3 = 0.33333.
3 / 6 = 1 / 2 = 0.55555.
4 / 6 = 2 / 3 = 0.66666.
5 / 6 = 1 / 6 + 4 / 6 = 0.16666666 + 0.6666666 = 0.833333333.
Fractions of 7 follow a special pattern and are arguably the most difficult ones, some memory space is needed. Here’s how:
1 / 7 = 0.142857 (Which continues to infinity).
2 / 7 = 0.285714 (Which also continues to infinity).
3 / 7 = 0.428571 (Which also continues to infinity).
4 / 7 = 0.571428 (Which also continues to infinity).
5 / 7 = 0.714285 (Which also continues to infinity).
6 / 7 = 0.857142 (Which also continues to infinity).
Fractions of 9 are simple in that they are repeated to infinity. Examples:
1 / 9 = 0.11111111111.
3 / 9 = 1 / 3 = 0.33333.
7 / 9 = 0.77777777777.
The pattern is always the same but changes place. To memorize it, think about it this way; the higher you go, the higher the number to start with. Check the pattern of the first numbers after the zero (1, 2, 4, 5, 7, 8). Therefore, with the above knowledge, the below fractional operations become simple:
(1 / 9) + (2 / 8) = 0.1111 + 0.25 ~ 0.361
(2 / 3) + (2 / 5) = 0.6666 + 0.40 ~ 1.066
(3 / 4) + (1 / 6) = 0.75 + 0.166 ~ 0.916
I have learnt some of the above techniques from a great book I have read years ago called Secrets of Mental Maths by Arthur Benjamin and Michael Shermer.
Subtracting from 1000
There is a quick trick we can use when subtracting from 1000. Here is an example:
1000–423 = 577 this is done by subtracting all the numbers on the left from 9 and subtracting the last number on the right from 10.
This gives us:
9–4 = 5
9–2= 7
10–3 = 7
Here is another example:
1000–758
Let us do the same thing as the above:
9–7 = 2
9–5 = 4
10–8 = 2
The result is therefore, 242.
Conclusion
Mental math is an impressive and useful technique that we all need to know. Mathematics form a huge part in our life and being able to be in tune with calculations will make us see the world from a completely different angle, plus it keeps the mind fresh by always making it work to find the result.