In the world of data science and machine learning, the quest to predict future outcomes is a fundamental challenge. This is particularly true when it comes to time series data, where patterns, trends, and seasonality play pivotal roles.
One of the powerful tools in our forecasting arsenal is AdaBoost, an ensemble learning method that has proven its mettle in a wide range of predictive tasks. In this article, we will embark on a journey into the realm of AdaBoost forecasting, exploring how this technique enhances the accuracy and robustness of time series predictions. We will use employment data from the US as an example.
Introduction to AdaBoost Algorithm
AdaBoost, short for Adaptive Boosting, is a machine learning algorithm that is part of what is known as ensemble models. Imagine you have a group of people (weak learners) who are not very good at solving a problem. Individually, each person might make mistakes, but collectively, they have some knowledge or insights. AdaBoost’s job is to take these individuals and make them work together effectively to solve the problem.
The steps that the algorithm follow can be summed up as follows (we’ll stick to a simple human example to illustrate the algorithm):
In the first round, AdaBoost asks each person (weak learner) to try and solve the problem. They might make some mistakes, but that’s okay, we all make mistakes.
After the first round, AdaBoost looks at the mistakes made by each person. It pays more attention to the mistakes and gives extra importance to the people who made them. It’s like saying, “You made a mistake last time; let’s see if you can do better this time.”
In the second round, AdaBoost again asks everyone to solve the problem. But this time, those who made mistakes in the first round get more attention. The idea is to focus on the areas where the individuals made mistakes before.
This process of evaluating mistakes and giving extra importance to the people who made mistakes continues for several rounds. In each round, AdaBoost adjusts the importance of individuals based on their past performance.
In the end, AdaBoost combines the solutions from all the individuals. But here’s the clever part: it gives more weight to the people who did well in the rounds where they previously made mistakes. It’s like saying, “You had a tough time at first, but you’ve improved, so we should trust you more now.”
The result is a combined solution that is often much better than what any single individual could achieve. By focusing on the areas where mistakes are made and adapting over time, AdaBoost can effectively solve complex problems.
So, in simple terms, AdaBoost is like training a group of individuals to work together on a problem, with a special focus on those who previously made mistakes, and combining their efforts to find a better solution. It’s a technique that can turn a group of weak learners into a strong learner when working together.
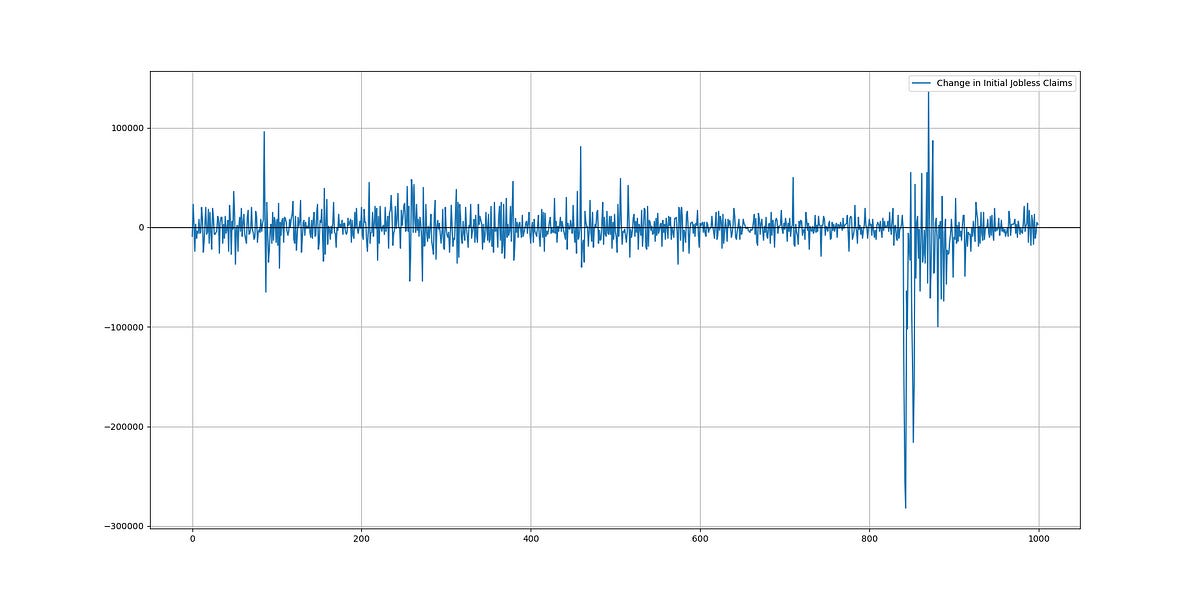
Before moving on to the algorithm, let’s discuss what we are trying to forecast. Initial jobless claims represent the number of individuals who have filed for unemployment benefits for the first time during a specific week. When people lose their jobs due to factors like layoffs or company closures, they file for these benefits with their state’s labor department, which serves as a financial safety net.
This data is reported on a weekly basis, allowing for timely assessment of changes in the job market. Economists, policymakers, and investors closely monitor these claims, as a significant increase in jobless claims can signal economic hardship and a weakening job market, while a decrease or stability in claims may indicate economic recovery or stability. The following chart shows the change in claims from one week to another.
If you want to see more of my work, you can visit my website for the books catalogue by simply following this link:
Creating the Algorithm
We will take the differences in the initial jobless claims and try to run them through AdaBoost to see how well it forecasts the next changes. The framework is as follows:
Import the jobless claims data from the federal reserve of Saint-Louis.
Difference, split, and fit the data using the regression model.
Predict and evaluate the results.
Use the following code to design the algorithm:
import numpy as np
from sklearn.ensemble import AdaBoostRegressor
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
def data_preprocessing(data, num_lags, train_test_split):
# Prepare the data for training
x = []
y = []
for i in range(len(data) - num_lags):
x.append(data[i:i + num_lags])
y.append(data[i+ num_lags])
# Convert the data to numpy arrays
x = np.array(x)
y = np.array(y)
# Split the data into training and testing sets
split_index = int(train_test_split * len(x))
x_train = x[:split_index]
y_train = y[:split_index]
x_test = x[split_index:]
y_test = y[split_index:]
return x_train, y_train, x_test, y_test
# Set the dates
start_date = '1970-01-01'
end_date = '2023-06-01'
# Prepare the data
data = np.array((pdr.get_data_fred('ICSA', start = start_date, end = end_date)).dropna())
data = np.reshape(data, (-1))
data = np.diff(data)
# Clean anomalous Covid data
data = np.delete(data, [2617, 2618, 2619, 2620, 2621, 2622, 2623, 2624, 2625, 2626], axis = 0)
'''
plt.plot(data[-1000:], label = 'Change in Initial Jobless Claims')
plt.axhline(y = 0, color = 'black', linewidth = 1)
plt.grid()
plt.legend()
'''
x_train, y_train, x_test, y_test = data_preprocessing(data, 900, 0.80)
# Create the model
model = AdaBoostRegressor(random_state = 0)
# Fit the model to the data
model.fit(x_train, y_train)
# Predict on the same data used for training
y_pred = model.predict(x_test)
# Plot the original sine wave and the predicted values
plt.plot(y_pred[-50:], label = 'Predicted Data', linestyle = '--', marker = 'o')
plt.plot(y_test[-50:], label = 'True Data', marker = 'o', alpha = 0.7)
plt.legend()
plt.grid()
plt.axhline(y = 0, color = 'black', linestyle = '--')
import math
from sklearn.metrics import mean_squared_error
rmse_test = math.sqrt(mean_squared_error(y_pred, y_test))
print(f"RMSE of Test: {rmse_test}")
same_sign_count = np.sum(np.sign(y_pred) == np.sign(y_test)) / len(y_test) * 100
print('Hit Ratio = ', same_sign_count, '%')The following chart shows a comparison between actual and predicted values. Note that the values are the change in the jobless claims.
The following shows the results of the model:
RMSE of Test: 33281.323321672724
Hit Ratio = 50.53191489361703 %AdaBoost is generally a very powerful model, but everything has its limitations especially with such a noisy time series like the initial claims. With an accuracy of 50.53%, certain questions remain to be asked:
What are the optimal independent variables for this task?
What is the optimal lag for the lagged variables?
What is the optimal train-test split?
You can also check out my other newsletter The Weekly Market Sentiment Report that sends weekly directional views every weekend to highlight the important trading opportunities using a mix between sentiment analysis (COT report, put-call ratio, etc.) and rules-based technical analysis.
If you liked this article, do not hesitate to like and comment, to further the discussion!