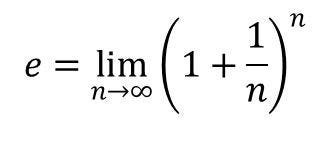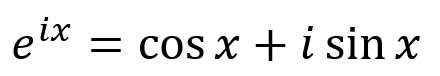13 Fascinating Numbers - When Beauty Meets Math
Numbers & Mathematical Concepts that Everybody Needs to Know
Sometimes, numbers are found using beautiful equations and formulas. They can also have mathematical beauty in that their properties offer a predictable outcome that is visually and intellectually appealing. From infinity to the Golden ratio, the below will discuss 13 of the fascinating numbers in nature.
13. Aleph Null ℵ0
Aleph Null is a beautiful concept. It is the smallest infinite number. I know what you’re thinking, infinity should be just one concept, not many infinite numbers. After all, if there is an infinity larger than the other infinity, the first one is definitely not an infinity.
Let’s suppose that we have a basic idea on what infinity is (discussed below, 12 in the list). Aleph null is how many natural numbers there are (0, 1, 2, 3, etc.). This concept or number is huge in size and well, infinite.
What if we count all of the natural numbers two or three times? After finishing the first set, we’ll have numbers that extend beyond the natural numbers in order. So, we will need the order of numbers, otherwise known as ordinality. The next number after Aleph Null is omega (ω), then comes ω + 1. These two last numbers are not cardinal numbers but ordinal, i.e. they represent their position compared to a horizontal axis. The below graph is a simplistic representation. Each set can represent the set of natural numbers in existence, and each set has the cardinality ℵ0. Adding one after the first set does not change the cardinality (You can just change the order and you’ll still be left with Aleph Null cardinality).
It helps to think of them as ordinals (order). Hence, the first ordinal transfinite number after a set is the one we’ve discussed above “ω”
You do not have omega apples, but you can be finishing omega in the race (If you’re really bad)
Interestingly, ω + 1 isn’t necessarily bigger than ω, it just comes after it. This is all a bit too much to take in, so puttings things in perspective should help. Here’s what we should know:
Infinity and Aleph Null are two different things. The former is simply an extreme limit idea lying on the number axis while the latter is simply the size of the set (cardinality).
Cardinality is the size of a set and cardinal numbers represent quantity (1, 2, 459, 1002, etc.) while Ordinality is the order of a set and ordinal numbers represent order (1st, 2nd, 66th, etc.).
Just as there are infinite cardinals, there are infinite ordinals as well and the first infinite (uncountable) ordinal number is the one we have discussed above, omega ω.
Following this logic, Aleph one is the cardinality of omega ω.
Aleph Null is just the first of a huge set of other “Alephs”. Vsauce has made an amazing video discussing this concept, which I heavily recommend.
12. Infinity ∞
Okay, so, this is more of an idea or a concept rather than a number. The symbol is often referred to as a lemniscate ∞ . An important thing before discussing the characteristics and fun facts about infinity is that the number pi (discussed down the list) is considered a form of infinity. Of course, by that, we mean the range of numbers after the dot 3.14159… This is why infinity is a concept and not something we’re able to quantify. Another example comes from the beautiful field of fractals. Take for example the simple Koch snowflake which can be subdivided into infinitesimal same shaped flakes.
Interestingly, when we think of infinity, we imagine an ever-growing measure, but it is not expanding or getting bigger. It is already what it is.
Let’s discuss two simple infinity-related topics (ones that do not require any brain activity because mine at this stage needs to take a nap after the Aleph Null and Infinity talks). Interestingly, Georg Cantor the father of set theory and research that dealt with infinities was institutionalized at many points in his life):
— — — Does 0.99999 = 1?
Naturally, the 0.99999 has 9’s that tend to go to infinity so approximately, we know for sure that it equals 1. Proving it algebraically is also possible:
If we have X = 0.9999 then
10X = 9.9999
If we subtract X from each side, we’d have
9X = 9.9999 -0.9999
9X = 9
Dividing by 9
X = 1
Weird, huh?
— — — Does ∞ — ∞ = 0?
Any number subtracted from itself will yield zero. But infinity is not a number. Hence, let’s try out a test:
∞ — ∞ = 0
∞ — ∞ + 1= 0 + 1 # Adding 1 to both sides
∞ — ∞ = 1 # Knowing that ∞ + 1 = ∞, we can simplify the equation
We’re left with a whole other result. Through this method we can get infinity minus infinity to equal any number we want. As such, the answer to ∞ — ∞ is undefined.
Finally, we are also taught that we cannot divide by 0. We are taught that 1 / 0 = Undefined, however, that is not false, but it doesn’t cover the full story. Think about it intuitively, if you divide 1 apple on 0 people, how many people would you need to cover the full apple? Naturally, it’s a form of infinity that never collapses.
So, originally, 1 / 0 = ∞. Why are we taught that the result is undefined? Simple, when we have 1 / small positive numbers that tend towards zero, it is simple to assume that 1 / 0 = ∞. The thing is, here, infinity is the positive infinity. And if we do 1 / small negative numbers that tend towards zero, we can also assume that 1 / 0 = -∞. So, which is it? Does 1 / 0 = ∞ or 1 / 0 = -∞? Well, the answer is undefined.
Conclusive table for operations on infinity:
∞ + ∞ = ∞
-∞ + -∞ = -∞
∞ × ∞ = ∞
-∞ × -∞ = ∞
-∞ × ∞ = -∞
11. i
The letter i refers to an imaginary number. The definition of an imaginary number is that when we square it, it gives us a negative result. This is not what we usually think about when squaring numbers because we know that multiplying two same symbols will always yield a posititve result. But this does not stop us from creating the axiom that inhibits the existence of such numbers. We call them imaginary because they shouldn’t exist. What is the square root of -6? We do not know. The calculator will give you an invalid input error because what two numbers do you multiply together to get a negative number? But the beauty of maths is that unlike other scientific tools, you can assum things to exist and tweak them to existence if they don’t work for you.
The concept of imaginary numbers is simple. We can assume (or imagine) that they exist. How are they useful? Well, we can solve equations that need a square root of a negative number. Here’s an example:
What is √4 ? Simple, it is 2.
What is √-4? A litte more complicated but the answer is 2i.
We add the i to represent the imaginary number to make 2 raised to the power of 2 equals -4. Let’s check out a very simple equation that normally does not have a solution and see how it is solved using imaginary numbers:
Obviously, x raised to the power of 2 can never give out a negative number (-1 in our case), so we just assume that the answer (as we did above) is multiplied by i.
You can think of the square root of -1 (√-1) as the original imaginary number. As in the number 1 for real numbers. Other uses for imaginary numbers is by combining them with natural numbers to make complex numbers (e.g. 7i + 12) and in electricity through matching currents.
10. Googol
A googol equals 10 followed by 100 zeros, therefore, to put things into perspective, think the following number: 10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000, or you can just be normal and think of it this way:
It is approximately 70! (Factorial). which is 70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59 …. x 1
To more complicate our minds, there exists a number called Googol plex, which is simply 10 to the power of Googol, written as:
It is interesting to note that the company Google is a misspelling of the Googol name. It is indeed a smart way to name your search engine. The number is mostly used with astronomical studies such as the big freeze of the universe.
9. The number 9 (Coincidentally ranked 9)
This is my favourite number and it’s probably for trading reasons but I also find it visually and mathematically beautiful. In geometry we tend to find it hidden in a many places, such as:
The circle. It has 360 degrees (3 + 6 + 0 = 9)
The circle cut in half. Each half is 180 degrees (1 + 8 + 0 = 9)
The circle cut in quarters. Each quarter is 90 degrees (9 + 0 = 9)
The circle cut in 8 pieces. Each part is 45 degrees (4 + 5 + 0 = 9)
The circle cut in 16 pieces. Each part is 22.5 degrees (2 + 2 + 5 = 9)
The circle cut in 32 pieces. Each part is 11.25 degrees (1 + 1 + 2 +5 = 9)
A regular polygon inside a circle. Each angle is 60 x 3 (180 = 1 + 8 = 9)
A square. Each angle is 90 x 4 (360 = 3 + 6 + 0 = 9)
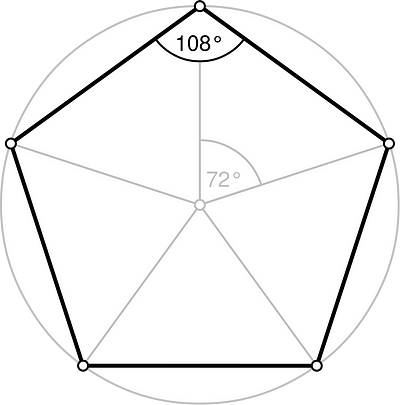
The following figures and their angles.
From left to right: Pentagon, Octagon, Decagon.
Pentagon = 108 = 1 + 0 + 8 = 9 // 72 = 7 + 2 = 9
Octagon =135 = 1 + 3 + 5 = 9 // 45 = 4 + 5 = 9
Decagon = 144 = 1 + 4 + 4 = 9 // 36 = 3 + 6 = 9
Also, If we add the digits that come before the number 9 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36). Then we’ll have as usual 3 + 6 = 9
Multiplying the digits that come before 9 and summing their elements will always give us 9, examples:
9 x 1 = 9
9 x 3 = 27 = 2 + 7 = 9
9 x 7 = 63 = 6 + 3 = 9
9 x 9 = 81 = 8 + 1 = 9
Dividing the digits by 9 will always give us the same digit repeated to infinity, examples:
1 / 9 = 0.11111
3 / 9 = 0.33333
7 / 9 = 0.77777
8. The number 73
If you’re a fan of The big bang Theory, then you must’ve heard Dr. Sheldon Cooper stating why 73 is the perfect number, here’s the quote:
“The best number is 73. Why? 73 is the 21st prime number. Its mirror, 37, is the 12th and its mirror, 21, is the product of multiplying 7 and 3.”’”
“In binary 73 is a palindrome, 1001001, which backwards is 1001001.”’
The quotes are taken from the show from Episode 10 season 4, which coincidentally is the 73rd episode of the show (and the year Jim Parsons the actor portraying Sheldon was born).
7. Euler’s number
Named after Leonhard Euler, e is an irrational number and the base of the natural logarithms. Interestingly, euler’s number is known to around 1 trillion digits of accuracy [source: mathisfun.com]. It is found following this formula:
As n approaches infinity, we get a clearer vision of the value of e. When n = 100,000, e = 2.71827. An interesting property that e has, is that its slope is its value. It is also used in finance to calculate compound interest. I believe those of you who have already taken the CFA test are familiar with this information.
6. The Fibonacci sequence
Leonardo Bonacci also known as Leonardo Fibonacci (which is a nickname to say son of Bonacci), has created one of the most fascinating series in our universe using simple addition techniques while observing rabbit populations. Now, to be fair, there is some evidence that suggest Indian mathematicians knew this sequence beforehand, we will stick to the widely accepted fact that Fibonacci came up with the sequence (Although, knowing the bright scientific and mathematical history of Indian researchers, I wouldn’t be surprised to know that they were the ones who discovered it first).
Fibonacci numbers are simply obtained using the following simple formula for n > 2:
This gives us the following sequence that goes to infinity:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ….
The beauty of this sequence is that it is related to nature. For example, it appears the flowering of the artichoke, some flower petals such as Daisies, honeybees, etc.. Does it even occur in the galaxy spirals?
There is even a very interesting observation based on facts that suggests that the dimensions of the Earth and Moon are in Phi relationship, forming a Triangle based on 1.618, by Gary Meisner. But what is Phi, and what is this 1.618?
If we take any two successive numbers in the sequence, their ratio (Xn / Xn-1) gets closer to 1.618 which is what we call the golden ratio:
3 / 2 = 1.5
13 / 8 = 1.666
55 / 34 = 1.61764
233 / 144 = 1.61805
…
317,811 / 196,418 = 1.61803
Going to infinity, the ratios get closer to 1.618, also known as Phi (ϕ). We will discuss Phi in greater details down the list.
5. The number 23
Many among us have seen the movie: the number 23 which features Jim Carrey portraying the persona of Walter Sparrow as someone who becomes obssessed with the number 23 after reading about it in a book. The belief here is that this number mysteriously coincides with many events all around the world and while that can be a perfect example of Apophenia, it is still interesting to list some events that have 23 embedded in them:
The 9/11 tragic events can sum up to 23 when we write the full date as the following: 9 + 11 + 2 + 0 + 0 + 1 = 23. Of course, we could have also did 9 + 11 + 2001 = 2021.
According to the Birthday paradox, 23 is the smallest number of randomly-selected people necessary to obtain at least 50% chance of having at least two people with the same birthday. For curiousity purposes, 70 people gives us 99.99% chance.
William Shakespeare was born on April 23rd, coindidentally, he died on April 23rd as well. of course, the date of birthday is not known for sure (He was baptized on the 26th), but it is widely believed to be the 23rd of April.
The Titanic sank on April 15th, 1912. Summing the full date (including April’s number) gives us 4 + 1 + 5 + 1 + 9 + 1 + 2 = 23. Of course, this is starting to resemble data snooping and digging for patterns because we are cherry-picking the dates to sum and the ones not to sum.
The Earth is inclined on its orbital plane by 23.5 degrees. We can consider the 5 as being 2 + 3, just to make things interesting. Of course, The earth’s axis of rotation is tilted 66.5 degrees to its orbital plane, but that’s not very cool to know.
The Arecibo message consists of 1679 bits, arranged into 73 lines of 23 characters per line. This is made-up by humans of course, but it is still interesting. The Arecibo message is a message sent from earth towards space in search for intelligent life. It sums up our life.
Humans have 23 pairs of chromosomes.
The sum of the first 23 primes is 874, which is divisible by 23. Thanks, Wikipedia.
The Hiroshima bomb was dropped at 8:15. 8 + 15 = Tragic event that tore up thousands of life. Also, 8 + 15 = 23.
23 is the lowest prime that consists of consecutive digits
The Knights Templar had 23 Grand Masters.
On average, the human blood circulates through the whole body every 23 seconds.
And lastly, the ordinal number of 23 on this list is 5, amounting again to 2 + 3, but that was made-up. Bottomline here is that even though numbers are beautiful, not all of them contain some mysterious elements. I think 23 is a little overhyped considering the evidence we have. In this list, there are many other numbers with far more interesting characteristics.
4. Pi (π) & Tau (τ)
The famous irrational number representing the ratio of circumference of a circle to its radius. Who among us hasn’t come across this number?
If we draw a circle with a diameter of 1, then the circumference will be equal to 3.14159… which is simply represented by the letter π. It is simply the circumference by the diameter. Now, we do not need to revisit middle school geometry concepts, so, I will just list two interesting properties of π:
Its digits go on to infinity with no pattern.
We all know the 22/7 approximation for Pie. But no ratio can give out the exact value of pie because it’s an irrational number.
Why did I include Tau? Some mathematicians have been debating the usefulness of π and propose Tau instead which is simply τ = 2π. Many mathematicians argue that Tau is more suited for calculating circles. Their intuition is correct when we want to dig into the details, but who doesn’t love Pi(e)?
A fun fact to mention is that there is a Pi day which is celebrated each year on the 14th of March (US date display is MM/DD, thus giving us 3/14).
3. Euler’s identity
This is why I have included the word “beauty” in the title. Combining some of the most beautiful concepts in maths can give us such simple results. Let’s recap first what concepts are we talking about and how are we going to combine them:
Euler’s number e
The unit imaginary number i
Pi π
It’s fascinating to see these three together form an equation such as the below to give us the simple result of -1.
How did we get -1 from the three musketeers?
As we have already seen together, i raised to the power of 2 = -1. Leonhard Euler applied the Taylor series with i giving him the following equation (omitting the details as they are beyond the scope of this article):
Putting the above Euler’s formula on a complex plane (with real numbers and imaginary ones) gives us a circle. By including a radius of r, we can turn the points into another form such as re raised to the power of ix.
If we assume x = π, then we will have the following:
Knowing that cos π = -1 and sin π = 0, then the i on the right will disappear:
So, we can also rearrange this equation to make it more beautiful and add another simple number:
2. The number 6174
Also known as Kaprekar’s constant, this number has a special feature if you follow the below steps (Taken from various sources, but let’s just say Wikipedia):
Take any four-digit number (at least two digits should be different).
Arrange the digits in descending and ascending order to get two new four-digit numbers.
Now, subtract the smaller number from the bigger number.
Redo step 2.
If you do this for multiple steps, you will always end up with 6174 and that is the mysterious thing about. Why do we always end up with this number no matter which numbers you start with. Let’s take an example of 2714:
7421 -1247 = 6174
Another example of 3687:
8763 -3678 = 5085;
8550 -0558 = 7992;
9972 -2799 = 7173;
7731 -1377 = 6354;
6543 -3456 = 3087;
8730 -0378 = 8352;
8532 -2358 = 6174
Now, if we have 6174, we will always stay at 6174 because 7641 -1467 = 6174.
It is also a Harshad number, meaning it is divisible by the sum of its constituents: 6174 / (6 + 1 + 7 + 4) = 6174 / 18 = 343. So, that adds to its coolness.
1. The golden ratio
We have already discussed this ratio, but it is probably the most important ratio in the world (It was named by the Greeks). Here’s a list of its characteristics:
The reciprocal of 0.618 is simply 1 + 0.618. Hence, 1 / ϕ ≈ 1 + ϕ
It appears in Nature (as previously mentioned). Some tree branches are an example. The main trunk will grow until it produces a branch thus creating two new starting points. One of the starting points will grow two others while the other will not. The pattern is similar to the Fibonacci pattern.
It is believed to represent Beauty and even though this belief is not proven, it remains interesting to know how our minds define beauty. For example, the face. Now, the following is probably not the most accurate research made but Dr. Schmid has a 10 scale ratio with 10 as the highest (most beautiful person) with most people scoring between 4 and 6. The beauty metric is first measured by the length and the width of the face then divides by the width. The optimal result is 1.618. Meaning a beautiful person’s face is 1.618 longer than it’s width. Later on, other ratios are calculated such as the bottom of the nose to the bottom of the chin. Finally, symmetry tests are performed to check out more beauty metrics. Dr. Schmid says that the length of the ear should be equal to the length of the nose on a perfect face, among other characteristics.
It is believed that the ratio of our arm to our forehand is equal to ϕ.
It is present in Geometry. Many buildings and artworks have the Golden Ratio in them, An example would be the Parthenon in Greece.
The pantagram has the golden ratio embedded inside of it.